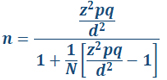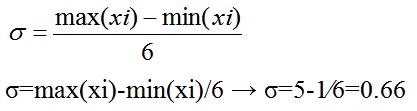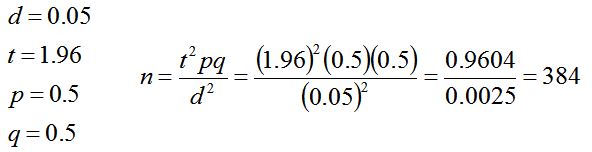تحلیل آماری پایان نامه در کم تر از 5 روز ! ویژه پایان نامه دکتری و کارشناسی ارشد
تحلیل آماری پایان نامه و مقالات علمی
آیا موعد تحویل پروپوزال، پایان نامه و یا دِدلاین مقاله تان نزدیک است؟
آیا با تحلیل آماری نتایج پایان نامه و مقاله خود به مشکل خورده اید؟
آیا برای تحلیل آماری پایان نامه و مقاله هزینه ی زیادی پرداخت کرده و نتیجه نگرفته اید؟!
آیا تحلیل آماری پایان نامه و مقاله شما را فرشود و کلافه کرده است!
اگر جواب این سوالات بلی است دست نگه دارید!
کافی است با ما تماس بگیرد و تا در کمترین زمان ممکن، با کیفیت ترین حالت و پایین ترین قیمت، مشکل شما را حل کنیم.
اگر هم اکنون این متن را میخوانید احتمالا استاد دانشگاه، محقق مراکز تحقیقاتی و یا دانشجوی دکترا یا کارشناسی ارشد هستید. مسلما شما در مراحل مختلف تحصیل آکادمیک برای تجزیه و تحلیل آماری پایان نامه، پروپوزال، مقاله و یا پروژههای تحقیقاتی نیاز به یک متخصص تحلیل آماری دارید.
اگر مهارت کافی در وارد نمودن اطلاعات، کدبندی و پایش آنرا ندارید و یا اینکه نمیدانید از کدام روش و چه نرم افزاری برای تجزیه و تحلیل اطلاعات خود استفاده نمایید، باید این را بدانید که تمامی این موارد به دانش زمینهای در حوزه روش تحقیق و آمار و نیز تجربه و تبحر کافی در استفاده از نرمافزارهای آماری برای تجزیه و تحلیل دادهها نیاز دارد.
تیم روا20 این نوید را به شما میدهد که برای تجزیه و تحلیل آماری پایان نامه، پروپوزال و مقاله خود بتوانید بدون هیچگونه اضطراب و نگرانی، متخصصین آماری را در کنار خود داشته باشید.
متخصصین ما در تمامی مراحل از ابتدای اجرای پژوهش و طراحی مطالعه، جمع آوری اطلاعات، نگارش پروپوزال و پایان نامه و تجزیه و تحلیل اطلاعات جمع آوری شده در کنار شما خواهند بود تا با خیال راحت بتوانید در مراحل مختلف آکادمیک خود موفق ظاهر شوید.
رسالت ما این است که به محققین، اساتید و دانشجویان داخل و خارج از کشور در ارتقا دانش، بهبود رزومه علمی و تحلیل آماری کمک نماییم و در شرایط مختلف خدمات متناسب با نیاز آماری آنها را برایشان فراهم آوریم.
هدف ما ارائه مشاوره و خدمات تحلیل آماری برای انجام یک تحقیق با کیفیت است. با استفاده از یک تحلیل آماری با کیفیت و متناسب با روشهای صحیح تجزیه و تحلیل میتوانید در وقت و هزینه خود صرفهجویی نموده و سریعتر به اهداف علمی خود برسید.
خدمات روا20
در روا20 خدمات مشاوره آماری، مشاوره در روش تحقیق، مشاوره در تعیین حجم نمونه و روش نمونه گیری، وارد نمودن اطلاعات در نرمافزارهای مختلف و نیز تجزیه و تحلیل آماری را به محققین، اساتید و دانشجویان داخل و خارج از کشور به منظور انجام پروژههای تحقیقاتی همانند پروپوزال، پرسشنامه، پایاننامه و مقالات علمی ارائه می گردد.
بدون هیچ نیازی به اینکه یک متخصص آمار باشید و یا کار با نرم افزارهای آماری را یاد داشته باشید. تنها نیاز است که پرسشنامه و یا دادهها و اطلاعات وارد شده به نرمافزار را برای ما ارسال نموده تا ما آنها را بر اساس اهداف و فرضیات مطالعه برای شما پایش نموده و آنالیز آماری مربوط با آن را برایتان انجام دهیم.
انجام تحلیل آماری پایان نامه، پروپوزال و مقالات علمی شما به وسیله متخصصین آماری خبره که دارای تجربه بیش از 20 سال در زمینه تجزیه و تحلیل هستند، انجام خواهد گرفت. تحلیل آماری و یا همان فصل4 نتایج شما به صورت کاملا تایپ شده به همراه فایل داده ها، خروجی نرم افزار، گزارش تحلیل شامل (آمار توصیفی و استنباطی ، توضیح و تفسیر نتایج آزمون ها، جداول، اشکال و نمودارهای مربوطه) ارائه خواهد گردید.
حوزه خدمات ارائه شده در وبسایت روا20 بسیار وسیع می باشد که عبارتند از :
مشاوره در نوشتن پایان نامه: مشاوره پایان نامه به ویژه برای نوشتن پروپوزال ، فصل های 1 ، 3، 4 و 5 که بسیار تخصصی و نیاز به مهارت خاص خود دارند.
پیشنهاد بسیار ویژه و ضروری: برای نوشتن پروپوزال و همچنین قبل از نوشتن فصل های 4 و 5 لازم است، تکلیف سوال ها / فرضیه ها ، متغیر ها و نقش آن ها در پژوهش / حجم و روش نمونه ی آماری ، ابزار استاندارد اندازه گیری و روش تحلیل داده های آماری 100 درصد و بدون هیچ گونه ابهامی مشخص شود و حتماً این موارد را به تأیید استاد راهنما برسانید و تا حد امکان یک نوشته یا صوت و … مبنی بر تأیید این موارد توسط وی را داشته باشید. چون هر گونه تغییر در آن ها شما را با چالش بزرگ روبرو خواهد کرد. سایر موارد پایان نامه و مقاله قابل ویرایش می باشد. اما برای ویرایش این موارد لازم است کل پژوهش بازنویسی و در آن تغییر ایجاد شود. لذا مواظب این قسمت ها باشید. بیشتر دانشجویان و محققان به این قسمت ها توجه نمی کنند. اینا مار خفته اند و ممکن است هر لحظه بیدار شوند و نیششان کشنده خواهد بود!
لذا ما در روا 20 سعی می کنیم برای دانشجو تا حد امکان این مشکلات پیش نیاید و کسانی که از ما در نوشتن پروپوزال کمک بگیرند، این مشکلات را در آتی نخواهند داشت. چون ما گربه را دم هجله می کشیم!
بنابراین در روند انجام یک پروپوزال از ابتدا متخصصین ما در مواردی همچون تعیین اهداف و فرضیات مطالعه، روش نمونهگیری و تعیین اندازه یا حجم نمونه، تعیین نوع مطالعه، مشخص نمودن ماهیت متغیرها و نگارش جدول متغیرها و نگارش بخش تحلیل آماری مطالعه به شما مشاوره خواهند داد.
تجزیه و تحلیل آماری پایان نامه : انجام تحلیل آماری مربوط به یک پژوهش ملزم به اجرای گام به گام مواردی همچون جمع آوری و شبیه سازی داده ها، پایش و کدگذاری اطلاعات و وارد کردن اطلاعات از پرسشنامه و یا چک لیست به نرمافزار، اجرای تحلیل در نرم افزار و انجام آمار توصیفی و استنباطی، نگارش بخش تحلیل آماری پایاننامه (فصل ۴) و تفسیر نتایج پایان نامه است که در روا20 تمامی مراحل فوق بسته به نیاز محقق قابل انجام است.
افراد زیادی هستند که تحلیل آماری انجام می دهند. اما کسی یا تیمی در این رابطه موفق هست که بتواند با انواع نرم افزارها کار کنید، کسانی که فقط با یکی دو مورد از نرم افزار ها کار می کنند، ممکن است شما را دچار مشکل کنند. چون دید وسیعی ندارند و وسعت دیدشان در قالب همین نرم افزار های محدود خواهد. امروز یک تحلیل گر آماری نه تنها با روش های کمی حتما باید با روش ها کیفی هم آشنایی داشته باشد. این را بدانید که spss نرم افزار بسیار قوی است ولی امروزه به تنهایی به هیچ وجه جوابگوی پژوهش گران نخواهد بود.
اگر دنبال تحلیل گر خوب هستید. حتما ابتدا ازش بپرسید که با انواع روش های تحلیل کیفی، کمی و آمیخته آشنایی دارد یا نه! تیم روا 20 امکان تحلیل را برای هر سه نوع تحلیل فراهم کرده است. ما تحلیل کمی را با نرم افزارهای spss , Amos , pls , excel , lisrel & … و فاز کیفی را با نرم افزارهای Maxqda , Nvivo و تحلیل آمیخته را با ترکیبی از این نرم افزارها انجام می دهیم.
تحلیل آماری مقالات : به دلیل اینکه در مقالات علمی تحلیلهای آماری باید به صورت جامع، خلاصه و محدودتر انجام گردد، نیاز به تجربه و تبحر کافی در انجام آنالیز آماری و نگارش آن است. متخصصین آماری در تیم روا20 در مورد تحلیل و چگونگی چینش جداول و نمودارها، نگارش نحوه نمونهگیری و تحلیل آماری در بخش موارد و روشها(Method)، تحلیل آماری و نگارش بخش نتایج(Result)، شبیه سازی اطلاعات مقاله و نیز ارائه و نگارش نتایج به زبان انگلیسی متناسب با مجلات انگلیسی زبان (ISI, PubMed, Scopus) به شما مشاوره خواهند داد.
مشاوره آماری جهت انجام آنالیز متناسب با دادهها : اگر محققی هستید که علاقهمندید خودتان تحلیل آماریتان را انجام دهید و تنها نیاز دارید بدانید از چه روش و تست آماری تجزیه و تحلیل دادهها باید انجام شود، متخصصین روا20 با توجه به ماهیت متغیرهای مربوطه، اهداف، فرضیات و عنوان مطالعه در این زمینه به شما مشاوره خواهند داد.
مشاوره آماری تحلیل انجام شده :اگر مشاور آماری یا استاد مشاور آمار مطالعه شما، تحلیل آماریتان را برایتان انجام داده است و شما برای دفاع پایان نامه و یا نظر داور یک مقاله نیاز دارید که آنالیز صورت گرفته را به صورت کامل متوجه شوید تا بتوانید ارائه مناسب و یا پاسخ مناسبی به داورد بدهید متخصصین روا20 به شما در مورد تحلیلهای انجام گرفته به صورت کامل مشاوره خواهند داد.
نگارش و تحلیل خروجی خام نرمافزار : در برخی موارد امکان دارد که مشاور آماری و یا استاد مشاور آماری پژوهش شما، خروجی تحلیلی نرمافزار را به صورت خام به شما تحویل داده است و شما نیاز دارید که این بخش به صورت کامل و جدولبندی شده به همراه نگارش استنباط این خروجی انجام شود. ما در روا20 پس از دریافت خروجی نرمافزار، تحلیل آن را به صورت کاملاً نگارش شده متناسب با بخش نتایج پایاننامه یا مقاله آماده خواهیم نمود.
تعیین روایی و پایایی ابزار مطالعه : قبل از شروع به جمعآوری اطلاعات در یک مطالعه یا پژوهش نیاز به بررسی متناسب و دقیق بودن ابزار و یا پرسشنامه مورد استفاده میباشد. ما در روا20 خدمات مربوط به بررسی روایی و پایایی انواع ابزار و پرسشنامه در مطالعات مختلف را ارائه میدهیم.
آموزش نرم افزار های آماری: تیم ما آموزش انواع نرم افزار ها را در سایت روا 20 و کانال آپارات آموزه 20 به صورت رایگان و بعضاً با قیمت بسیار پایین جهت استفاده محققین گرامی گذاشته است.
ارائه انواع پرسشنامه استاندارد: با توجه به تجربه بیش از 20 ساله دریافته ایم که پژوهشگران به ویژه پژوهشگران حوزه ی علوم انسانی در این خصوص مشکلات بسیاری دارند. در سال های اخیر سایت ها فایل فروشی به صورت بسیار زیادی و قارچ گونه بوجود آمده اند. هدف اغلب این سایت ها فروش فایل هست! در حالیکه پرسشنامه یک ابزار علمی است و باید تمامی موارد از جمله روش نمره گذاری، اعتبار سنجی، پایایی، روایی و منبع نویسی داخل و پایان متن کاملاً مشخص و به صورت علمی نوشته شده باشد و گرنه پژوهشگر را با چالش بزرگ مواجه خواهد کرد، اما فایل فروش ها به این موارد توجه نمی کنند و تقریباً هیچ یک از این موارد در فایل آن ها لحاظ نشده است، تیم روا20 برای حل این مشکل اقدام به تهیه و جمع آوری ، اعتبار سنجی و … پرسشنامه ها نموده و آن ها را در قالب فایل ورد و بدون هیچ گونه تبلیغ و یا مورد اضافه ای که باعث سردرگمی پژوهشگران به ویژه دانشجویان تازه کار درآورده است . فعلا این پرسشنامه ها در 3 برگه ارائه شد . به علت حساسیتی که روی این موضوع داریم فعلاً کار به کندی پیش می رود ولی در حال تکمیل هست. اگر شما پرسشنامه ای نیاز داشتید که در سایت نبود می توانید با ما تماس بگیرید و آن را سفارش دهید تا نسخه ی علمی و قابل استفاده آن را برایتان تهیه کنیم.
نکته مهم: از هر جایی به ویژه فایل فروش های فله ای برای پژوهشتان پرسشنامه نخرید و خودتان را از چاله به چاه نیندازید! از ما گفتن بود!
وارد نمودن داده ها و اطلاعات از پرسشنامه و یا چکلیست به نرم افزار : از آنجایی که وارد نمودن دادهها و اطلاعات به نرمافزارهای مختلف آماری نیاز به آشنایی با ماهیت متغیرها، نقش متغیرها، برچسب گذاری متغیرها، کدبندی اطلاعات و تعیین مقیاس متغیرها در یک مطالعه دارد، متخصصین خبره روا20 در این مهم شما را یاری خواهند نمود. خدمات وارد نمودن اطلاعات، کدگذاری، تعیین ماهیت و نقش متغیرها و نیز برچسب گذاری آنها در انواع نرمافزارهای آماری از جلمه Excell، SPSS و …. در روا20 قابل انجام است.”
در تهیه پاورپونت دفاعیه چه مطالبی را باید قرار بدهم تا یک دفاع عالی از پایان نامه داشته باشم؟
نوشته
برای تحلیل عاملی تأییدی از چه نرم افزار های آماری می توان استفاده کرد؟
نوشته
وفاداری مشتری: ارزش و اهمیت بیپایان در تجارت مدرن
نوشته
صفحه روی جلد پایان نامه شامل چه مواردی می شود؟
نوشته
برترین سایت های خارجی برای دانلود پایان نامه های دانشگاه های اروپایی و آمریکایی