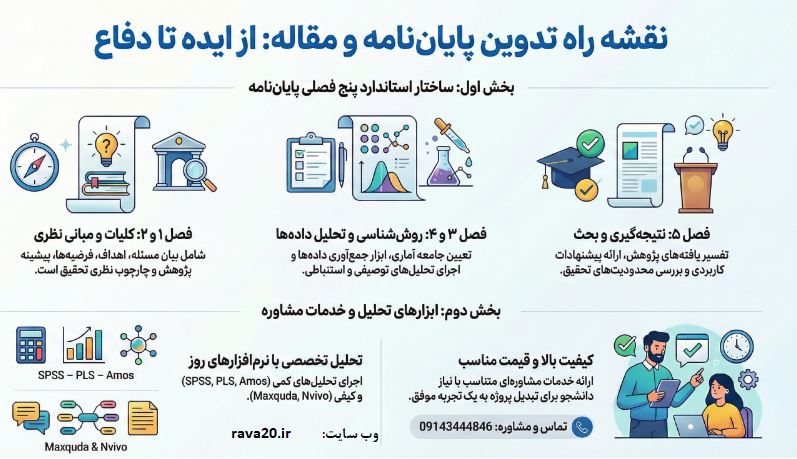
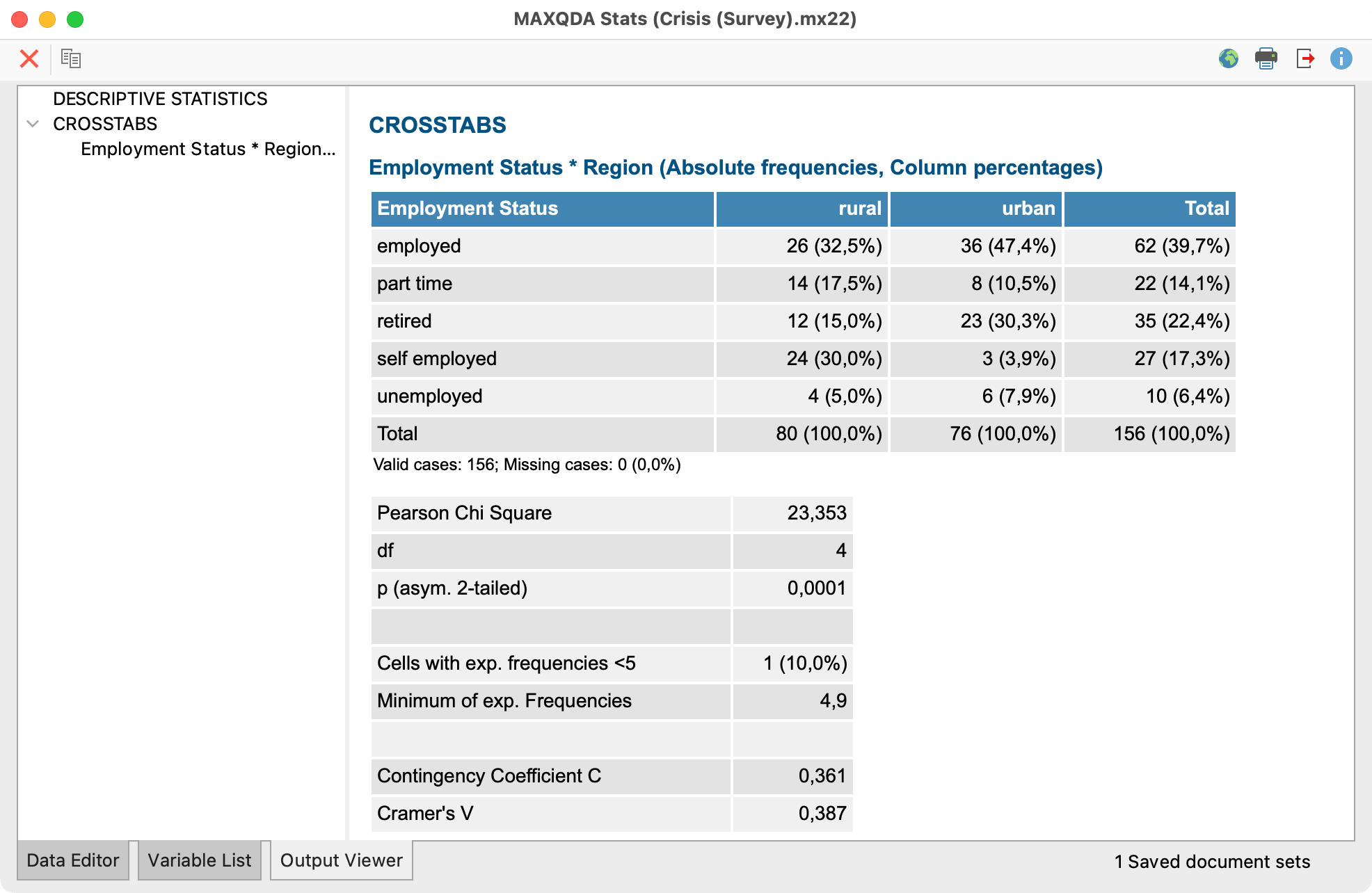
آزمون ANOVA و معادل ناپارامتریک: راهنمای جامع انتخاب، اجرا و تفسیر

آیا برای مقایسه سه گروه یا بیشتر سردرگم هستید که ANOVA استفاده کنید یا کراسکال-والیس؟ انتخاب اشتباه بین این آزمون‌ها، اعتبار پژوهش شما را مخدوش می‌کند. در این راهنمای جامع، تمام آزمون‌های تحلیل واریانس (ANOVA یک‌طرفه، دوطرفه، اندازه‌گیری مکرر) و معادل‌های ناپارامتریک آنها را با جدول مقایسه، فرمول‌ها، پیش‌فرض‌ها، درخت تصمیم‌گیری و مثال‌های واقعی بررسی می‌کنیم.

---

🔍 آزمون ANOVA و معادل ناپارامتریک چیست؟

تحلیل واریانس (ANOVA) خانواده‌ای از آزمون‌های پارامتریک است که میانگین سه گروه یا بیشتر را مقایسه می‌کند. معادل‌های ناپارامتریک مانند کراسکال-والیس و فریدمن، میانه یا رتبه داده‌ها را بدون نیاز به نرمال بودن مقایسه می‌کنند.

انتخاب صحیح بین این دو، تضمین‌کننده اعتبار آماری پژوهش شماست.

---

📊 دسته‌بندی کامل آزمون‌های ANOVA و معادل ناپارامتریک

نوع طرح پژوهش	آزمون پارامتریک	آزمون ناپارامتریک معادل	تعداد متغیر مستقل	نوع گروه‌ها
سه گروه یا بیشتر مستقل	One-Way ANOVA	کراسکال-والیس (Kruskal-Wallis)	۱	مستقل
سه گروه یا بیشتر وابسته	Repeated Measures ANOVA	فریدمن (Friedman)	۱	وابسته
دو عامل مستقل	Two-Way ANOVA	شییر-ری-هیر (Scheirer-Ray-Hare)	۲	مستقل
دو عامل وابسته	Two-Way RM ANOVA	معادل ناپارامتریک وجود ندارد	۲	وابسته
متغیر وابسته دوتایی	—	کاکرن Q (Cochran’s Q)	۱ یا بیشتر	وابسته
چند متغیر وابسته	MANOVA	معادل قدرتمند وجود ندارد	۱ یا بیشتر	مستقل/وابسته

---

✅ آزمون ANOVA یک‌طرفه و معادل ناپارامتریک

🔵 آزمون پارامتریک: تحلیل واریانس یک‌طرفه (One-Way ANOVA)

کاربرد: مقایسه میانگین سه یا چند گروه مستقل.

مثال واقعی: آیا میانگین نمرات درس آمار در دانشجویان سه رشته روانشناسی، علوم تربیتی و مشاوره تفاوت معناداری دارد؟

پیش‌فرض‌های حیاتی:

• متغیر وابسته در سطح فاصله‌ای یا نسبی باشد.
• نرمال بودن توزیع داده‌ها در هر گروه.
• همگنی واریانس‌ها (برابری واریانس گروه‌ها).
• استقلال مشاهدات.
• عدم وجود پرت‌های تأثیرگذار.

فرمول آماره F:
$𝐹=\frac{𝑀{𝑆}_{𝑏𝑒𝑡𝑤𝑒𝑒𝑛}}{𝑀{𝑆}_{𝑤𝑖𝑡ℎ𝑖𝑛}}=\frac{\frac{𝑆{𝑆}_{𝑏𝑒𝑡𝑤𝑒𝑒𝑛}}{𝑑{𝑓}_{𝑏𝑒𝑡𝑤𝑒𝑒𝑛}}}{\frac{𝑆{𝑆}_{𝑤𝑖𝑡ℎ𝑖𝑛}}{𝑑{𝑓}_{𝑤𝑖𝑡ℎ𝑖𝑛}}}$F=MSwithin​MSbetween​​=dfwithin​SSwithin​​dfbetween​SSbetween​​​

درجات آزادی:
$𝑑{𝑓}_{𝑏𝑒𝑡𝑤𝑒𝑒𝑛}=𝑘-1$dfbetween​=k−1
$𝑑{𝑓}_{𝑤𝑖𝑡ℎ𝑖𝑛}=𝑁-𝑘$dfwithin​=N−k

آزمون‌های تعقیبی (Post Hoc):

• توکی (Tukey): برای حجم نمونه برابر.
• شفه (Scheffe): محافظه‌کارانه، مناسب حجم‌های نابرابر.
• بونفرونی (Bonferroni): تنظیم سطح آلفا برای مقایسه‌های متعدد.

🟢 معادل ناپارامتریک: آزمون کراسکال-والیس (Kruskal-Wallis)

کاربرد: مقایسه میانه یا توزیع سه یا چند گروه مستقل.

زمان استفاده:

• داده‌ها نرمال نیستند.
• داده‌ها در سطح رتبه‌ای هستند (مقیاس لیکرت).
• حجم نمونه در برخی گروه‌ها کوچک است.
• واریانس‌ها ناهمگن هستند.

مکانیسم محاسبه:

1. تمام داده‌های همه گروه‌ها را ترکیب کنید.
2. به همه مشاهدات رتبه بدهید (از کوچک به بزرگ).
3. مجموع رتبه‌های هر گروه را محاسبه کنید (Rᵢ).
4. آماره H را محاسبه کنید:

$𝐻=\frac{12}{𝑁(𝑁+1)}{\sum }_{𝑖=1}^{𝑘}\frac{{𝑅}_{𝑖}^2}{{𝑛}_{𝑖}}-3(𝑁+1)$H=N(N+1)12​∑i=1k​ni​Ri2​​−3(N+1)

پیش‌فرض‌ها:

• متغیر وابسته حداقل در سطح رتبه‌ای باشد.
• نمونه‌ها مستقل و تصادفی باشند.
• توزیع گروه‌ها باید شکل مشابهی داشته باشند (برای تفسیر میانه).

⚠️ هشدار مهم: اگر توزیع گروه‌ها شکل متفاوتی داشته باشد، کراسکال-والیس صرفاً نشان می‌دهد «توزیع‌ها متفاوت هستند». نمی‌توان نتیجه گرفت که «میانه‌ها متفاوت هستند».

آزمون‌های تعقیبی:

• آزمون دان (Dunn’s Test) با تصحیح بونفرونی.
• آزمون من-ویتنی با تصحیح بونفرونی.

---

✅ آزمون ANOVA با اندازه‌گیری مکرر و معادل ناپارامتریک

🔵 آزمون پارامتریک: ANOVA با اندازه‌گیری مکرر (Repeated Measures ANOVA)

کاربرد: مقایسه میانگین سه یا چند اندازه‌گیری وابسته از یک گروه.

مثال واقعی: آیا میانگین سطح استرس افراد در سه زمان قبل از امتحان، حین امتحان و بعد از امتحان تفاوت معناداری دارد؟

پیش‌فرض‌های حیاتی:

• متغیر وابسته در سطح فاصله‌ای یا نسبی باشد.
• نرمال بودن توزیع تفاوت‌ها بین زمان‌ها.
• کرویت (Sphericity): برابری واریانس تفاوت‌ها بین تمام جفت‌زمان‌ها.
• عدم وجود پرت‌های تأثیرگذار.

آزمون کرویت (Mauchly’s Test):

• اگر p > 0.05: شرط کرویت برقرار است.
• اگر p < 0.05: شرط کرویت نقض شده است.

تصحیحات در صورت نقض کرویت:

• گرین‌هاوس-گایسر (Greenhouse-Geisser): برای انحراف شدید از کرویت.
• هاین-فلدت (Huynh-Feldt): برای انحراف ملایم از کرویت.

🟢 معادل ناپارامتریک: آزمون فریدمن (Friedman Test)

کاربرد: مقایسه میانه سه یا چند اندازه‌گیری وابسته.

زمان استفاده:

• داده‌ها در سطح ترتیبی هستند (مقیاس لیکرت).
• پیش‌فرض نرمال بودن تفاوت‌ها نقض شده است.
• حجم نمونه کوچک است.
• شرط کرویت برقرار نیست.

مکانیسم محاسبه:

1. برای هر آزمودنی، به مقادیر شرایط مختلف رتبه بدهید (از ۱ تا k).
2. مجموع رتبه‌های هر ستون (شرط) را محاسبه کنید (Rⱼ).
3. آماره Fr یا χ² را محاسبه کنید:

${𝜒}_{𝑟}^2=\frac{12}{𝑛𝑘(𝑘+1)}{\sum }_{𝑗=1}^{𝑘}{𝑅}_{𝑗}^2-3𝑛(𝑘+1)$χr2​=nk(k+1)12​∑j=1k​Rj2​−3n(k+1)

پیش‌فرض‌ها:

• متغیر وابسته حداقل در سطح ترتیبی باشد.
• نمونه‌ها به صورت تصادفی انتخاب شده باشند.
• بلوک‌ها (آزمودنی‌ها) مستقل از یکدیگر باشند.

⚠️ هشدار بسیار مهم: تحقیقات نشان داده است آزمون فریدمن توان آماری بسیار پایینی دارد و عملاً معادل آزمون علامت است، نه ویلکاکسون.

✅ راه‌حل: از ANOVA بر روی رتبه‌ها (Repeated Measures ANOVA on Ranks) استفاده کنید که توان آماری بالاتری دارد.

آزمون‌های تعقیبی:

• آزمون ویلکاکسون جفتی با تصحیح بونفرونی.
• آزمون علامت با تصحیح بونفرونی.

---

✅ آزمون ANOVA دوطرفه و معادل ناپارامتریک

🔵 آزمون پارامتریک: تحلیل واریانس دوطرفه (Two-Way ANOVA)

کاربرد: بررسی همزمان اثر دو عامل مستقل و اثر تعاملی آنها بر یک متغیر وابسته.

مثال واقعی: بررسی اثر جنسیت (مرد/زن) و روش تدریس (سنتی/الکترونیکی/تلفیقی) بر نمرات تحصیلی.

پیش‌فرض‌های حیاتی:

• متغیر وابسته در سطح فاصله‌ای یا نسبی باشد.
• نرمال بودن توزیع داده‌ها در هر ترکیب از گروه‌ها.
• همگنی واریانس‌ها بین تمام سلول‌ها.
• استقلال مشاهدات.

خروجی اصلی:

• اثر اصلی عامل اول (Factor A)
• اثر اصلی عامل دوم (Factor B)
• اثر تعاملی (A × B)

🟢 معادل ناپارامتریک: آزمون شییر-ری-هیر (Scheirer-Ray-Hare Test)

کاربرد: معادل ناپارامتریک ANOVA دوطرفه برای داده‌های غیرنرمال یا رتبه‌ای.

زمان استفاده:

• پیش‌فرض نرمال بودن داده‌ها نقض شده است.
• داده‌ها در سطح رتبه‌ای هستند.
• واریانس‌ها ناهمگن هستند.

مکانیسم محاسبه:

1. به تمام داده‌ها رتبه بدهید (بدون توجه به گروه‌بندی).
2. تحلیل واریانس دوطرفه را روی رتبه‌ها انجام دهید.
3. مجموع مربعات (SS) هر منبع را بر مجموع مربعات کل بر اساس رتبه تقسیم کنید.
4. آماره H = SS / MS_total را محاسبه کرده و با توزیع کای-دو آزمون کنید.

پیش‌فرض‌ها:

• طرح متوازن (Balanced Design) ترجیح داده می‌شود.
• حداقل ۵ مشاهده در هر سلول برای اثر تعاملی توصیه می‌شود.

⚠️ محدودیت‌ها:

• این آزمون برای اثرات تعاملی توان آماری پایینی دارد.
• برخی آماردانان ANOVA با رتبه‌های ترازشده (Aligned Ranks Transformation ANOVA) را توصیه می‌کنند.

🔴 تذکر مهم: ANOVA دوطرفه با اندازه‌گیری مکرر

هیچ آزمون ناپارامتریک واقعی برای ANOVA دوطرفه با اندازه‌گیری مکرر وجود ندارد.

راه‌حل‌های جایگزین:

• تبدیل رتبه‌ای داده‌ها و اجرای ANOVA پارامتریک.
• استفاده از مدل‌های خطی تعمیم‌یافته (GLM).

---

✅ آزمون‌های تخصصی دیگر

🟣 آزمون کاکرن Q (Cochran’s Q)

کاربرد: معادل ناپارامتریک ANOVA با اندازه‌گیری مکرر برای متغیرهای وابسته دوتایی (باینری).

مثال: مقایسه نسبت موفقیت یک روش درمانی در سه زمان مختلف (موفق/ناموفق).

پیش‌فرض‌ها:

• متغیر وابسته دوتایی (۰ و ۱) است.
• گروه‌ها وابسته هستند (همان آزمودنی‌ها).
• نمونه‌ها تصادفی انتخاب شده‌اند.

🟣 MANOVA و معادل ناپارامتریک

کاربرد: مقایسه همزمان چند متغیر وابسته بین گروه‌ها.

معادل ناپارامتریک:

• معادل قدرتمند و شناخته‌شده‌ای وجود ندارد.
• راه‌حل‌های جایگزین: تبدیل رتبه‌ای چندمتغیره، بوت‌استرپ، یا آزمون‌های جداگانه با تصحیح آلفا.

---

📋 جدول مقایسه جامع آزمون‌های ANOVA و معادل ناپارامتریک

معیار مقایسه	ANOVA یک‌طرفه	کراسکال-والیس	RM ANOVA	فریدمن	Two-Way ANOVA	شییر-ری-هیر
شاخص مرکزی	میانگین	میانه/توزیع	میانگین	میانه	میانگین	میانه/توزیع
سطح اندازه‌گیری	فاصله‌ای/نسبی	رتبه‌ای/فاصله‌ای	فاصله‌ای/نسبی	ترتیبی/فاصله‌ای	فاصله‌ای/نسبی	رتبه‌ای/فاصله‌ای
نوع گروه‌ها	مستقل	مستقل	وابسته	وابسته	مستقل	مستقل
نرمال بودن	✅ الزامی	❌ نیازی نیست	✅ الزامی	❌ نیازی نیست	✅ الزامی	❌ نیازی نیست
همگنی واریانس	✅ الزامی	❌ (شکل مشابه)	کرویت الزامی	❌ نیازی نیست	✅ الزامی	❌ نیازی نیست
حساسیت به پرت	بسیار بالا	پایین	بسیار بالا	پایین	بسیار بالا	پایین
توان آماری	بالاتر	~95% ANOVA	بالاتر	پایین	بالاتر	متوسط
آزمون تعقیبی	توکی، شفه، بونفرونی	دان، من-ویتنی	توکی، بونفرونی	ویلکاکسون، علامت	توکی، شفه	دان، من-ویتنی
اثر تعاملی	—	—	—	—	✅ قابل محاسبه	✅ قابل محاسبه
پشتیبانی SPSS	کامل	کامل	کامل	کامل	کامل	محدود

---

⚠️ تله‌های آماری که باید جدی بگیرید!

🎯 تله ۱: توان پایین آزمون فریدمن

تحقیقات معتبر نشان داده است که آزمون فریدمن توان آماری بسیار پایینی دارد و عملاً معادل آزمون علامت است.

✅ راه‌حل: از ANOVA بر روی رتبه‌ها (ANOVA on Ranks) استفاده کنید.

🎯 تله ۲: تفسیر کراسکال-والیس با توزیع‌های نامشابه

اگر توزیع گروه‌ها شکل متفاوتی داشته باشد:

• ❌ نمی‌گوییم: «میانه گروه A بزرگتر از گروه B است».
• ✅ می‌گوییم: «توزیع نمرات در گروه A به طور معناداری متفاوت از گروه B است».

🎯 تله ۳: ANOVA دوطرفه ناپارامتریک وجود ندارد!

تأکید می‌کنیم: ANOVA دوطرفه ناپارامتریک واقعی با گروه‌های وابسته وجود ندارد.

🎯 تله ۴: فراموش کردن آزمون‌های تعقیبی

ANOVA و کراسکال-والیس تنها نشان می‌دهند آیا تفاوتی وجود دارد یا خیر. اما کدام گروه‌ها با هم متفاوت هستند را مشخص نمی‌کنند.

🎯 تله ۵: نقض پیش‌فرض کرویت در RM ANOVA

همیشه:

1. آزمون Mauchly’s Test را بررسی کنید.
2. اگر p < 0.05، از تصحیحات گرین‌هاوس-گایسر یا هاین-فلدت استفاده کنید.

---

🧭 درخت تصمیم‌گیری: کدام آزمون ANOVA را انتخاب کنیم؟

textCopyDownload

چند گروه داریم؟
├── سه گروه یا بیشتر → ادامه
└── دو گروه → از آزمون‌های تی استفاده کنید

گروه‌ها مستقل هستند یا وابسته؟
├── مستقل → One-Way ANOVA یا Kruskal-Wallis
└── وابسته → RM ANOVA یا Friedman

چند متغیر مستقل داریم؟
├── یک عامل → آزمون‌های یک‌طرفه
└── دو عامل → Two-Way ANOVA یا Scheirer-Ray-Hare

آیا داده‌ها فاصله‌ای/نسبی و نرمال هستند؟
├── ✅ بله (و واریانس‌ها همگن) → ANOVA پارامتریک
└── ❌ خیر (یا رتبه‌ای هستند) → آزمون ناپارامتریک

آیا متغیر وابسته دوتایی است؟
├── ✅ بله (وابسته) → Cochran's Q
└── ❌ خیر → سایر آزمون‌ها

---

💡 نکات طلایی برای گزارش نتایج در مقاله

✅ گزارش صحیح ANOVA یک‌طرفه:

نتایج ANOVA یک‌طرفه نشان داد که میانگین نمرات در سه گروه آموزشی تفاوت معناداری دارد؛ F(2, 87) = 5.67, p = 0.005, η² = 0.12. آزمون تعقیبی توکی نشان داد که گروه A (M = 82.3, SD = 6.2) به طور معناداری نمرات بالاتری از گروه C (M = 74.1, SD = 7.5) دارد (p = 0.003).

✅ گزارش صحیح کراسکال-والیس:

آزمون کراسکال-والیس تفاوت معناداری را در رضایت شغلی بین سه گروه نشان داد (H(2) = 14.32, p = 0.001). آزمون تعقیبی دان نشان داد که میانگین رتبه گروه A (Mean Rank = 34.7) به طور معناداری بیشتر از گروه B (Mean Rank = 21.3) است (p = 0.002).

✅ گزارش صحیح RM ANOVA:

نتایج ANOVA با اندازه‌گیری مکرر نشان داد که سطح اضطراب در سه زمان اندازه‌گیری تفاوت معناداری دارد؛ F(2, 58) = 12.34, p < 0.001, η² = 0.30. آزمون تعقیبی بونفرونی نشان داد که اضطراب پس از مداخله (M = 32.4, SD = 6.7) به طور معناداری کمتر از پیش‌آزمون (M = 51.2, SD = 8.3) بود (p < 0.001).

✅ گزارش صحیح فریدمن:

آزمون فریدمن نشان داد که میانه نمرات درد در چهار زمان اندازه‌گیری تفاوت معناداری دارد (χ²(3) = 18.45, p < 0.001). آزمون تعقیبی ویلکاکسون با تصحیح بونفرونی نشان داد که شدت درد در زمان ۲۴ ساعت پس از جراحی (Mdn = 7) به طور معناداری بیشتر از زمان ۷۲ ساعت (Mdn = 3) بود (p = 0.002).

✅ گزارش صحیح Two-Way ANOVA:

نتایج ANOVA دوطرفه اثر معناداری برای جنسیت (F(1, 56) = 8.23, p = 0.006, η² = 0.13) و روش تدریس (F(2, 56) = 7.89, p = 0.001, η² = 0.22) نشان داد. اثر تعاملی جنسیت × روش تدریس معنادار نبود (F(2, 56) = 1.23, p = 0.30).

---

🎯 سناریوهای بالینی و پژوهشی

سناریوی ۱: مقایسه اثربخشی سه روش درمانی بر اضطراب

• طرح: سه گروه مستقل (درمان A، درمان B، کنترل)
• داده‌ها: نمرات اضطراب (فاصله‌ای)، نرمال، واریانس‌ها همگن
• انتخاب درست: One-Way ANOVA + آزمون تعقیبی توکی

سناریوی ۲: مقایسه رضایت بیماران (لیکرت ۵ درجه) در چهار بیمارستان

• طرح: چهار گروه مستقل
• داده‌ها: رتبه‌ای، توزیع نامشخص
• انتخاب درست: Kruskal-Wallis + آزمون تعقیبی دان

سناریوی ۳: تأثیر مداخله آموزشی بر پیشرفت تحصیلی در چهار زمان

• طرح: اندازه‌گیری مکرر (قبل، بعد، ۱ ماه بعد، ۳ ماه بعد)
• داده‌ها: نرمال، اما شرط کرویت نقض شده
• انتخاب درست: Repeated Measures ANOVA + تصحیح گرین‌هاوس-گایسر

سناریوی ۴: مقایسه کیفیت زندگی در سه زمان با داده‌های بسیار چوله

• طرح: اندازه‌گیری مکرر (سه زمان)
• داده‌ها: توزیع بسیار چوله، حجم نمونه کوچک
• انتخاب درست: Friedman Test + آزمون تعقیبی ویلکاکسون

سناریوی ۵: بررسی اثر همزمان جنسیت و سطح تحصیلات بر درآمد

• طرح: دو عامل مستقل (۲×۳)
• داده‌ها: نرمال، واریانس‌ها همگن
• انتخاب درست: Two-Way ANOVA

سناریوی ۶: بررسی اثر کود و آبیاری بر محصول کشاورزی (داده‌های غیرنرمال)

• طرح: دو عامل مستقل (۳×۲)
• داده‌ها: غیرنرمال، حجم سلول‌ها ≥۵
• انتخاب درست: Scheirer-Ray-Hare Test

سناریوی ۷: مقایسه موفقیت درمان (موفق/ناموفق) در سه زمان

• طرح: اندازه‌گیری مکرر با متغیر دوتایی
• داده‌ها: باینری (۰ و ۱)
• انتخاب درست: Cochran’s Q Test

---

❓ سؤالات متداول (FAQ)

سؤال ۱: اگر نتایج ANOVA و کراسکال-والیس متفاوت باشند، کدام را قبول کنم؟

اگر داده‌ها واقعاً نرمال هستند و واریانس‌ها همگن، ANOVA اعتبار بیشتری دارد. در غیر این صورت، کراسکال-والیس نتیجه قابل اعتمادتری است.

سؤال ۲: آیا می‌توانم برای مقیاس لیکرت ۷ درجه‌ای از ANOVA استفاده کنم؟

اگر تعداد طبقات ≥۷ و توزیع نسبتاً نرمال باشد، ANOVA معمولاً قابل قبول است. اما از نظر تئوری، داده‌های لیکرت رتبه‌ای هستند و آزمون ناپارامتریک مناسب‌تر است.

سؤال ۳: چرا آزمون فریدمن توان آماری پایینی دارد؟

زیرا فریدمن فقط رتبه‌ها را درون هر بلوک مقایسه می‌کند و اندازه تفاوت‌ها را نادیده می‌گیرد. این مشابه آزمون علامت است، نه ویلکاکسون.

سؤال ۴: بهترین آزمون تعقیبی برای کراسکال-والیس چیست؟

آزمون دان (Dunn’s Test) با تصحیح بونفرونی، استاندارد طلایی است.

سؤال ۵: چگونه اندازه اثر را برای آزمون‌های ناپارامتریک گزارش کنم؟

• برای کراسکال-والیس: ε² (epsilon-squared) یا η² بر اساس رتبه‌ها
• برای فریدمن: Kendall’s W (ضریب تطابق کندال)
• برای آزمون‌های تعقیبی: r = Z/√N

---

🚀 جمع‌بندی نهایی

✅ ANOVA یک‌طرفه را انتخاب کنید اگر:

• داده‌ها فاصله‌ای/نسبی و نرمال هستند.
• واریانس‌ها همگن هستند.
• حجم نمونه کافی است (>۱۵ در هر گروه).

✅ کراسکال-والیس را انتخاب کنید اگر:

• داده‌ها نرمال نیستند یا رتبه‌ای هستند.
• واریانس‌ها ناهمگن هستند.
• حجم نمونه کوچک است.

✅ RM ANOVA را انتخاب کنید اگر:

• همان افراد در چند زمان اندازه‌گیری شده‌اند.
• داده‌ها نرمال هستند.
• شرط کرویت برقرار است (یا تصحیح می‌شود).

✅ فریدمن را انتخاب کنید اگر:

• همان افراد در چند زمان اندازه‌گیری شده‌اند.
• داده‌ها رتبه‌ای یا غیرنرمال هستند.
• حجم نمونه بسیار کوچک است.

✅ ANOVA دوطرفه را انتخاب کنید اگر:

• دو عامل مستقل دارید.
• داده‌ها نرمال و واریانس‌ها همگن هستند.

✅ شییر-ری-هیر را انتخاب کنید اگر:

• دو عامل مستقل دارید.
• داده‌ها نرمال نیستند یا رتبه‌ای هستند.

---

💬 نظر شما چیست؟

آیا تاکنون در انتخاب بین ANOVA و آزمون‌های ناپارامتریک دچار تردید شده‌اید؟
آیا تجربه استفاده از آزمون شییر-ری-هیر را داشته‌اید؟
چه چالشی در تحلیل داده‌های اندازه‌گیری مکرر داشته‌اید؟

دیدگاه‌ها، تجربیات و سؤالات خود را در بخش نظرات با ما و دیگر پژوهشگران به اشتراک بگذارید.

به سه نظر برتر، مشاوره رایگان تحلیل آماری با SPSS هدیه داده می‌شود!

---

📞 ارتباط با تیم تخصصی راوا (Rava20.ir)

برای دریافت مشاوره تخصصی تحلیل آماری پایان‌نامه، مقاله‌نویسی ISI، آموزش نرم‌افزارهای آماری (SPSS, AMOS, PLS, maxqda) و طراحی پرسشنامه‌های استاندارد، از راه‌های زیر با ما در ارتباط باشید:

🌐 وب سایت: https://rava20.ir
📱 کانال تلگرام: https://t.me/RAVA2020
🎬 کانال آموزشی آپارات: https://www.aparat.com/amoozeh20
✍️ وبلاگ تخصصی: http://abazizi.parsiblog.com/

پرسشنامه آسیب به خود،   SHI (  سانسون و همکاران ، 1998 )

نکات مهم و ضروری در طراحی پرسشنامه طیف لیکرت

پرسشنامه اعتماد به نفس شراگر (PEI): دانلود + تفسیر کامل

انواع آزمون های پارامتریک و ناپارامتریک

پرسشنامه ارزیابی دانش، نگرش و عملکرد (KAP) پرستاران در برنامه‌ریزی ترخیص بیماران سکته مغزی

آزمون های تی ( t-test ) و معادل ناپارامتریک آن ها: راهنمای جامع انتخاب، اجرا و تفسیر

آیا می‌دانید چه زمانی باید از آزمون تی استفاده کنید و چه موقع سراغ من-ویتنی یا ویلکاکسون بروید؟ انتخاب اشتباه بین این آزمون‌ها، یکی از رایج‌ترین دلایل رد مقاله در مجلات معتبر است. در این راهنمای جامع، تمام آزمون‌های تی و معادل‌های ناپارامتریک آنها را با جدول مقایسه، مثال‌های واقعی و درخت تصمیم‌گیری بررسی می‌کنیم.

---

🔍 آزمون تی و معادل ناپارامتریک چیست؟

آزمون‌های تی (t-tests) خانواده‌ای از آزمون‌های پارامتریک هستند که میانگین یک یا دو گروه را مقایسه می‌کنند. معادل‌های ناپارامتریک آنها، مانند من-ویتنی و ویلکاکسون، میانه یا رتبه داده‌ها را بدون نیاز به نرمال بودن مقایسه می‌کنند.

انتخاب صحیح بین این دو، اعتبار آماری پژوهش شما را تضمین می‌کند.

---

📊 دسته‌بندی کامل آزمون‌های تی و معادل ناپارامتریک

نوع مقایسه	آزمون پارامتریک (تی)	آزمون ناپارامتریک معادل	پیش‌فرض اصلی آزمون تی
یک گروه با مقدار ثابت	One-Sample t-test	• Wilcoxon Signed-Rank (اولویت) • Sign Test (جایگزین)	نرمال بودن داده‌ها
دو گروه مستقل	Independent Samples t-test	• Mann-Whitney U (Wilcoxon Rank-Sum) • Kolmogorov-Smirnov	نرمال بودن + همگنی واریانس
دو گروه وابسته (جفتی)	Paired Samples t-test	• Wilcoxon Signed-Rank • Sign Test	نرمال بودن تفاوت جفت‌ها

---

✅ آزمون تی تک‌نمونه‌ای (One-Sample t-test)

🔵 آزمون پارامتریک: تی تک‌نمونه‌ای

کاربرد: مقایسه میانگین یک گروه با یک عدد ثابت یا هنجار جامعه.

مثال واقعی: آیا میانگین نمرات درس روش تحقیق دانشجویان روانشناسی (68 نفر) با میانگین فرضی 75 تفاوت معناداری دارد؟

پیش‌فرض‌های حیاتی:

• متغیر وابسته در سطح فاصله‌ای یا نسبی باشد.
• داده‌ها نرمال باشند.
• مشاهدات مستقل باشند.
• پرت تأثیرگذار وجود نداشته باشد.

فرمول:
$𝑡=\frac{\overline{𝑥}-{𝜇}_0}{𝑠\mathrm{/}\sqrt{𝑛}}$t=s/n​xˉ−μ0​​

درجه آزادی: df = n – 1

🟢 معادل ناپارامتریک: آزمون ویلکاکسون تک‌نمونه‌ای

کاربرد: مقایسه میانه یک گروه با یک مقدار ثابت.

زمان استفاده:

• داده‌ها نرمال نیستند.
• حجم نمونه کوچک است (کمتر از 30).
• داده‌ها در سطح رتبه‌ای هستند.

پیش‌فرض: توزیع تفاوت‌ها باید متقارن حول میانه باشد.

🔴 جایگزین ضعیف‌تر: آزمون علامت (Sign Test)

مکانیسم: فقط جهت مثبت یا منفی بودن داده‌ها را شمارش می‌کند.

⚠️ هشدار: این آزمون اندازه تفاوت‌ها را نادیده می‌گیرد. در نتیجه توان آماری بسیار پایینی دارد. فقط زمانی استفاده کنید که توزیع تفاوت‌ها به شدت نامتقارن باشد.

---

✅ آزمون تی دو گروه مستقل (Independent Samples t-test)

🔵 آزمون پارامتریک: تی مستقل

کاربرد: مقایسه میانگین دو گروه کاملاً مجزا.

مثال واقعی: آیا میانگین فشار خون در گروه داروی جدید با گروه دارونما تفاوت معناداری دارد؟

پیش‌فرض‌های حیاتی:

پیش‌فرض	روش بررسی	راهکار در صورت نقض
نرمال بودن	شاپیرو-ویلک یا کولموگروف-اسمیرنوف	استفاده از من-ویتنی
همگنی واریانس‌ها	آزمون لون (Levene)	تی ولش یا من-ویتنی
استقلال مشاهدات	طراحی مطالعه	—
عدم وجود پرت	نمودار جعبه‌ای (Boxplot)	تبدیل داده یا آزمون ناپارامتریک

فرمول (حالت استاندارد):
$𝑡=\frac{{\overline{𝑥}}_1-{\overline{𝑥}}_2}{\sqrt{\frac{{𝑠}_1^2}{{𝑛}_1}+\frac{{𝑠}_2^2}{{𝑛}_2}}}$t=n1​s12​​+n2​s22​​​xˉ1​−xˉ2​​

فرمول درجه آزادی (تقریب ولش برای واریانس ناهمگن):
$𝑑𝑓=\frac{(\frac{{𝑠}_1^2}{{𝑛}_1}+\frac{{𝑠}_2^2}{{𝑛}_2}{)}^2}{\frac{(\frac{{𝑠}_1^2}{{𝑛}_1}{)}^2}{{𝑛}_1-1}+\frac{(\frac{{𝑠}_2^2}{{𝑛}_2}{)}^2}{{𝑛}_2-1}}$df=n1​−1(n1​s12​​)2​+n2​−1(n2​s22​​)2​(n1​s12​​+n2​s22​​)2​

🟢 معادل ناپارامتریک: آزمون من-ویتنی یو (Mann-Whitney U)

کاربرد: مقایسه توزیع یا میانه دو گروه مستقل.

مکانیسم محاسبه گام‌به‌گام:

1. تمام داده‌های دو گروه را با هم ترکیب کنید.
2. به همه داده‌ها رتبه بدهید (از کوچک به بزرگ).
3. مجموع رتبه‌های هر گروه را محاسبه کنید (R₁ و R₂).
4. آماره U را محاسبه کنید:

${𝑈}_1={𝑛}_1{𝑛}_2+\frac{{𝑛}_1({𝑛}_1+1)}{2}-{𝑅}_1$U1​=n1​n2​+2n1​(n1​+1)​−R1​
${𝑈}_2={𝑛}_1{𝑛}_2+\frac{{𝑛}_2({𝑛}_2+1)}{2}-{𝑅}_2$U2​=n1​n2​+2n2​(n2​+1)​−R2​

5. آماره نهایی: U = min(U₁, U₂)

پیش‌فرض‌های کلیدی من-ویتنی:

• متغیر وابسته حداقل در سطح رتبه‌ای باشد.
• دو نمونه مستقل و تصادفی باشند.
• توزیع دو گروه باید شکل مشابهی داشته باشند (فقط از نظر موقعیت جابجا شده باشند).

⚠️ هشدار بسیار مهم: اگر توزیع دو گروه شکل متفاوتی داشته باشد، آزمون من-ویتنی صرفاً می‌گوید «توزیع‌ها متفاوت هستند» و نمی‌توان نتیجه گرفت که میانه‌ها متفاوت هستند.

🟡 معادل دیگر: آزمون کولموگروف-اسمیرنوف دو نمونه‌ای

این آزمون نسبت به من-ویتنی به شکل توزیع حساستر است، اما توان آماری کمتری دارد.

---

✅ آزمون تی جفتی (Paired Samples t-test)

🔵 آزمون پارامتریک: تی جفتی

کاربرد: مقایسه میانگین دو اندازه‌گیری وابسته (قبل-بعد، چپ-راست، همسان‌سازی شده).

مثال واقعی: آیا نمرات اضطراب بیماران قبل و بعد از 10 جلسه رفتاردرمانی شناختی تفاوت معناداری دارد؟

پیش‌فرض حیاتی: تفاوت جفت‌ها باید نرمال باشد. (نه خود داده‌ها!)

فرمول:
$𝑡=\frac{\overline{𝑑}}{{𝑠}_{𝑑}\mathrm{/}\sqrt{𝑛}}$t=sd​/n​dˉ​

$\bar{d}$ = میانگین تفاوت‌ها
$s_d$ = انحراف معیار تفاوت‌ها
$n$ = تعداد جفت‌ها

🟢 معادل ناپارامتریک: آزمون ویلکاکسون جفتی (Wilcoxon Signed-Rank)

کاربرد: مقایسه میانه تفاوت‌ها در دو گروه وابسته.

مکانیسم محاسبه:

1. تفاوت هر جفت را محاسبه کنید (dᵢ = yᵢ – xᵢ).
2. قدر مطلق تفاوت‌ها را رتبه‌بندی کنید.
3. رتبه‌ها را بر اساس علامت مثبت یا منفی تفاوت جدا کنید.
4. آماره V = مجموع رتبه‌های مثبت (یا منفی).

پیش‌فرض: توزیع تفاوت‌ها باید متقارن حول میانه باشد.

🔴 جایگزین ضعیف: آزمون علامت جفتی (Paired Sign Test)

تنها مزیت: زمانی که توزیع تفاوت‌ها به شدت نامتقارن است و شرط تقارن ویلکاکسون نقض شده، این آزمون قابل استفاده است.

عیب بزرگ: توان آماری بسیار پایین.

---

📋 جدول مقایسه جامع آزمون تی و معادل ناپارامتریک

معیار مقایسه	آزمون تی	آزمون من-ویتنی / ویلکاکسون
شاخص مرکزی	میانگین	میانه یا توزیع
سطح اندازه‌گیری	فاصله‌ای/نسبی (الزامی)	رتبه‌ای/فاصله‌ای/نسبی
پیش‌فرض نرمال بودن	✅ الزامی	❌ نیازی نیست
پیش‌فرض همگنی واریانس	✅ الزامی (جز تی ولش)	❌ نیازی نیست
حساسیت به پرت	بسیار بالا	پایین
توان آماری (در حالت نرمال)	بالاتر	~95% آزمون تی
حجم نمونه ایده‌آل	>30	<30 یا داده غیرنرمال
حداقل P-value ممکن	پیوسته (هر مقداری)	گسسته (دارای حداقل)
خروجی اصلی	t، df، p-value	U یا V، p-value
اندازه اثر	Cohen’s d	r = Z/√N یا Probabilistic Index

---

⚠️ تله‌های آماری که باید جدی بگیرید!

🎯 تله ۱: آزمون من-ویتنی با توزیع‌های نامشابه

اگر توزیع دو گروه شکل متفاوتی داشته باشد:

• ❌ نمی‌گوییم: «میانه گروه A بزرگتر از گروه B است».
• ✅ می‌گوییم: «توزیع نمرات در گروه A به طور معناداری متفاوت از گروه B است».

🎯 تله ۲: حداقل P-value در نمونه‌های کوچک

برای دو نمونه با حجم‌های 4 و 3، آزمون من-ویتنی نمی‌تواند p-value کمتر از 0.057 تولید کند!

یعنی حتی اگر تفاوت فاحش باشد، در سطح 0.05 معنادار نمی‌شود.

راه‌حل: حجم نمونه را افزایش دهید یا از آزمون‌های دقیق (Exact Tests) استفاده کنید.

🎯 تله ۳: ویلکاکسون با توزیع نامتقارن

اگر توزیع تفاوت‌ها در آزمون ویلکاکسون جفتی نامتقارن باشد، نتایج گمراه‌کننده خواهد بود.

راه‌حل: از آزمون علامت استفاده کنید یا داده‌ها را تبدیل نمایید.

🎯 تله ۴: تعدیل برای مقایسه‌های متعدد

اگر بعد از ANOVA یا کروسکال-والیس، چندین آزمون من-ویتنی انجام می‌دهید، حتماً تصحیح بونفرونی یا سایر روش‌های تعدیل را اعمال کنید.

---

🧭 درخت تصمیم‌گیری: آزمون تی یا ناپارامتریک؟

textCopyDownload

آیا داده‌ها فاصله‌ای/نسبی هستند؟
├── ❌ خیر (رتبه‌ای هستند) → آزمون ناپارامتریک
└── ✅ بله → سوال بعد

آیا حجم نمونه >30 است؟
├── ❌ خیر → بررسی نرمال بودن
└── ✅ بله → آزمون تی (طبق قضیه حد مرکزی)

آیا توزیع داده‌ها نرمال است؟
├── ✅ بله → آزمون تی
└── ❌ خیر → آزمون ناپارامتریک

آیا پرت تأثیرگذار وجود دارد؟
├── ✅ بله → آزمون ناپارامتریک
└── ❌ خیر → آزمون تی (در صورت نرمال بودن)

آیا واریانس‌ها همگن هستند؟ (فقط دو گروه مستقل)
├── ✅ بله → آزمون تی مستقل استاندارد
└── ❌ خیر → تی ولش یا من-ویتنی

---

💡 نکات طلایی برای گزارش نتایج در مقاله

✅ گزارش صحیح آزمون تی مستقل:

میانگین نمرات در گروه آزمایش (M=78.45, SD=6.32) به طور معناداری بیشتر از گروه کنترل (M=68.23, SD=7.11) بود؛ t(58)=4.23, p=0.001, d=0.89.

✅ گزارش صحیح آزمون من-ویتنی:

نتایج آزمون من-ویتنی نشان داد که رضایت بیماران در بیمارستان A (Mean Rank=34.7) به طور معناداری بیشتر از بیمارستان B (Mean Rank=21.3) است؛ U=112.5, Z=-3.45, p=0.001, r=0.42.

✅ گزارش صحیح آزمون تی جفتی:

میانگین اضطراب پس از درمان (M=34.2, SD=6.8) در مقایسه با پیش‌آزمون (M=52.7, SD=8.3) کاهش معناداری نشان داد؛ t(29)=8.67, p<0.001, d=1.58.

✅ گزارش صحیح آزمون ویلکاکسون جفتی:

آزمون ویلکاکسون نشان داد که میانه نمرات افسردگی پس از مداخله (Mdn=12) به طور معناداری کمتر از پیش‌آزمون (Mdn=24) است؛ V=23.5, p=0.002, r=0.53.

---

🎯 سناریوهای بالینی و پژوهشی

سناریوی ۱: مقایسه فشار خون دو گروه دارو و دارونما

• داده‌ها: نرمال، واریانس‌ها برابر
• انتخاب درست: Independent Samples t-test
• دلیل: پیش‌فرض‌ها برقرار و آزمون تی توان بالاتری دارد.

سناریوی ۲: مقایسه رضایت بیماران (لیکرت ۷ درجه)

• داده‌ها: رتبه‌ای، توزیع نامشخص
• انتخاب درست: Mann-Whitney U Test
• دلیل: داده‌ها فاصله‌ای نیستند.

سناریوی ۳: تأثیر مداخله آموزشی بر اضطراب (قبل-بعد)

• داده‌ها: تفاوت نمرات نرمال نیست، پرت وجود دارد
• انتخاب درست: Wilcoxon Signed-Rank Test
• دلیل: به پرت حساس نیست و از رتبه‌ها استفاده می‌کند.

سناریوی ۴: مقایسه نمرات هوش ۱۰ کودک با میانگین جامعه

• داده‌ها: حجم نمونه بسیار کوچک
• انتخاب درست: One-Sample Wilcoxon Signed-Rank Test
• دلیل: برای n=10 نمی‌توان به نرمال بودن اطمینان کرد.

---

📝 خلاصه: قانون ۳۰ ثانیه‌ای انتخاب آزمون

اگر…	پس آزمون مناسب…
داده‌ها نرمال هستند + حجم نمونه کافی است	آزمون تی
داده‌ها نرمال نیستند + حجم نمونه کوچک است	معادل ناپارامتریک
داده‌ها رتبه‌ای هستند	معادل ناپارامتریک
پرت‌های تأثیرگذار وجود دارد	معادل ناپارامتریک
واریانس‌ها ناهمگن هستند (دو گروه)	تی ولش یا من-ویتنی
می‌خواهم میانگین را مقایسه کنم	آزمون تی
می‌خواهم میانه را مقایسه کنم	معادل ناپارامتریک

---

❓ سؤالات متداول (FAQ)

سؤال ۱: آیا با حجم نمونه ۲۰۰، باز هم نیاز به بررسی نرمال بودن دارم؟

خیر. طبق قضیه حد مرکزی، با حجم نمونه بالای ۳۰، توزیع میانگین‌ها نرمال می‌شود و می‌توانید از آزمون تی استفاده کنید.

سؤال ۲: چرا نتایج آزمون تی و من-ویتنی گاهی متفاوت می‌شوند؟

زیرا آزمون تی میانگین را مقایسه می‌کند و من-ویتنی میانه یا توزیع را. اگر توزیع داده‌ها چوله باشد یا پرت وجود داشته باشد، این دو می‌توانند نتایج متفاوتی بدهند.

سؤال ۳: کدام آزمون قدرتمندتر است؟

اگر پیش‌فرض‌ها برقرار باشند، آزمون تی قدرتمندتر است. اما اگر پیش‌فرض‌ها نقض شوند، آزمون ناپارامتریک اعتبار بیشتری دارد.

سؤال ۴: آیا می‌توانم هم آزمون تی و هم ناپارامتریک را انجام دهم؟

خیر. این کار باعث افزایش خطای نوع اول می‌شود. بر اساس شرایط، یکی را انتخاب و گزارش کنید.

---

🚀 جمع‌بندی نهایی

✅ آزمون تی را انتخاب کنید اگر:

• داده‌ها فاصله‌ای/نسبی و نرمال هستند.
• حجم نمونه بزرگ است (>30).
• واریانس‌ها همگن هستند (برای دو گروه مستقل).
• پرت تأثیرگذار وجود ندارد.

✅ معادل ناپارامتریک را انتخاب کنید اگر:

• داده‌ها نرمال نیستند.
• حجم نمونه کوچک است.
• داده‌ها رتبه‌ای هستند.
• پرت‌های تأثیرگذار وجود دارند.
• واریانس‌ها ناهمگن هستند.

---

💬 نظر شما چیست؟

آیا تاکنون در انتخاب بین آزمون تی و من-ویتنی دچار تردید شده‌اید؟
چه تجربه‌ای از گزارش این آزمون‌ها در مقالات دارید؟

دیدگاه‌ها و سؤالات خود را در بخش نظرات با ما و دیگر پژوهشگران به اشتراک بگذارید.
به سه نظر برتر، مشاوره رایگان تحلیل آماری هدیه داده می‌شود!

---

📞 ارتباط با تیم تخصصی راوا

🌐 وب سایت: https://rava20.ir
📱 کانال تلگرام: https://t.me/RAVA2020
🎬 کانال آموزشی آپارات: https://www.aparat.com/amoozeh20
✍️ وبلاگ تخصصی: http://abazizi.parsiblog.com/

در طراحی و تدوین پرسشنامه رعایت چه نکاتی ضروری است.

تعریف عملیاتی متغیر های پژوهش به چه صورت می باشد؟

محاسبه آن لاین اثر میانجی با آزمون های سوبل، آریون و گودمن

پرسشنامه ویژگی های معلم اثربخش درآموزش مجازی

پرسشنامه  شایستگی دیجیتال بتین و همکاران (2023)