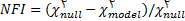نرم افزار لیزرل و انجام مدلسازی معادلات ساختاری با آن
1- مدل معادلات ساختاری چیست؟
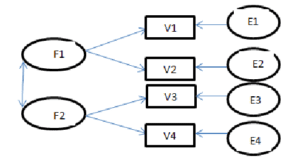
مدل يابي معادلات ساختاري (Structural equation modeling: SEM) يک تکنيک تحليل چند متغيري بسيار کلي و نيرومند از خانواده رگرسيون چند متغيري و به بيان دقيقتر بسط “مدل خطي کلي” (General linear model) یا GLM است. SEM به پژوهشگر امکان ميدهد مجموعه اي از معادلات رگرسيون را به صورت هم زمان مورد آزمون قرار دهد.
مدل يابي معادله ساختاري يک رويکرد جامع براي آزمون فرضيههايي درباره روابط متغيرهاي مشاهده شده و مکنون است که گاه تحليل ساختاري کوواريانس، مدل يابي علّي و گاه نيز ليزرل (Lisrel) ناميده شده است اما اصطلاح غالب در اين روزها، مدل يابي معادله ساختاري يا به گونه خلاصه SEM است. (هومن 1384،11)
از نظر آذر (1381) نيز يکي از قويترين و مناسبترين روشهاي تجزيه و تحليل در تحقيقات علوم رفتاري و اجتماعي، تجزيه و تحليل چند متغيره است زيرا اين گونه موضوعات چند متغيره بوده و نمي توان آنها را با شيوه دو متغيري (که هر بار يک متغير مستقل با يک متغير وابسته در نظر گرفته ميشود) حل نمود.
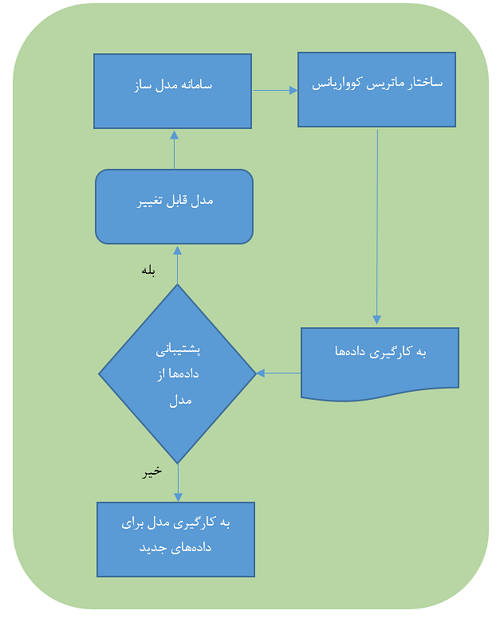
«تجزيه و تحليل ساختارهاي کوواريانس» يا همان «مدل يابي معادلات ساختاري»، يکي از اصليترين روشهاي تجزيه و تحليل ساختار دادههاي پيچيده و يکي از روشهاي نو براي بررسي روابط علت و معلولي است و به معني تجزيه و تحليل متغيرهاي مختلفي است که در يک ساختار مبتني بر تئوري، تاثيرات همزمان متغيرها را به هم نشان ميدهد. از طريق اين روش ميتوان قابل قبول بودن مدلهاي نظري را در جامعههاي خاص با استفاده از دادههاي همبستگي، غير آزمايشي و آزمايشي آزمود.
2- انديشه اساسي و زيربنايی مدل يابي ساختاري
يکي از مفاهيم اساسي که در آمار کاربردي در سطح متوسط وجود دارد اثر انتقالهاي جمع پذير و ضرب پذير در فهرستي از اعداد است. يعني اگر هر يک از اعداد يک فهرست در مقدار ثابت K ضرب شود ميانگين اعداد در همان K ضرب ميشود و به اين ترتيب، انحراف معيار استاندارد در مقدار قدر مطلق K ضرب خواهد شد.
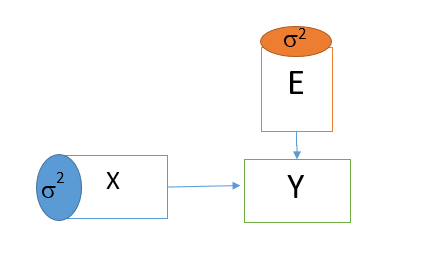
نکته اين است که اگر مجموعه اي از اعداد X با مجموعه ديگري از اعداد Y از طريق معادله Y=4X مرتبط باشند در اين صورت واريانس Y بايد 16 برابر واريانس X باشد و بنابراين از طريق مقايسه واريانسهاي X و Y ميتوانيد به گونه غير مستقيم اين فرضيه را که Y و X از طريق معادله Y=4X با هم مرتبط هستند را بيازماييد.
اين انديشه از طريق تعدادي معادلات خطي از راههاي مختلف به چندين متغير مرتبط با هم تعميم داده ميشود. هرچند قواعد آن پيچيدهتر و محاسبات دشوارتر ميشود، اما پيام کلي ثابت ميماند. يعني با بررسي واريانسها و کوواريانسهاي متغيرها ميتوانيد اين فرضيه را که “متغيرها از طريق مجموعه اي از روابط خطي با هم مرتبط اند” را بيازماييد.
توسعه مدلهاي علّي و همگرايي روشهاي اقتصادسنجي، روان سنجي و غیره
توسعه مدلهاي علّي متغيرهاي مکنون معرف همگرايي سنتهاي پژوهشي نسبتا مستقل در روان سنجي، اقتصادسنجي، زيست شناسي و بسياري از روشهاي قبلا آشناست که آنها را به شکل چهارچوبي وسيع در ميآورد. مفاهيم متغيرهاي مکنون (Latent variables) در مقابل متغيرهاي مشاهده شده (Observed variables) و خطا در متغيرها، تاريخي طولاني دارد.
در اقتصادسنجي آثار جهت دار هم زمان چند متغير بر متغيرهاي ديگر، تحت برچسب مدلهاي معادله همزمان بسيار مورد مطالعه قرار گرفته است. در روان سنجي به عنوان تحليل عاملي و تئوري اعتبار توسعه يافته و شالوده اساسي بسياري از پژوهشهاي اندازه گيري در روانسنجي ميباشد. در زيست شناسي، يک سنت مشابه همواره با مدلهاي معادلات همزمان (گاه با متغيرهاي مکنون) در زمينه نمايش و طرح برآورده در تحليل مسير سر و کار دارد.
3- موارد کاربرد روش ليزرل
روش ليزرل ضمن آنکه ضرايب مجهول مجموعه معادلات ساختاري خطي را برآورد ميکند براي برازش مدلهايي که شامل متغيرهاي مکنون، خطاهاي اندازه گيري در هر يک از متغيرهاي وابسته و مستقل، عليت دو سويه، هم زماني و وابستگي متقابل ميباشد طرح ريزي گرديده است.
اما اين روش را ميتوان به عنوان موارد خاصي براي روشهاي تحليل عاملي تاييدي، تحليل رگرسيون چند متغيري، تحليل مسير، مدلهاي اقتصادي خاص دادههاي وابسته به زمان، مدلهاي برگشت پذير و برگشت ناپذير براي دادههاي مقطعي/ طولي، مدلهاي ساختاري کوواريانس و تحليل چند نمونه اي (مانند آزمون فرضيههاي برابري ماتريس کوواريانس هاي، برابري ماتريس همبستگي ها، برابري معادلات و ساختارهاي عاملي و غيره) نيز به کار برد.
4- نرم افزار ليزرل چیست؟
ليزرل يک محصول نرم افزاري است که به منظور برآورد و آزمون مدلهاي معادلات ساختاري طراحي و از سوي “شرکت بين المللي نرم افزار علمي”
Scientific software international (www.ssicentral.com)
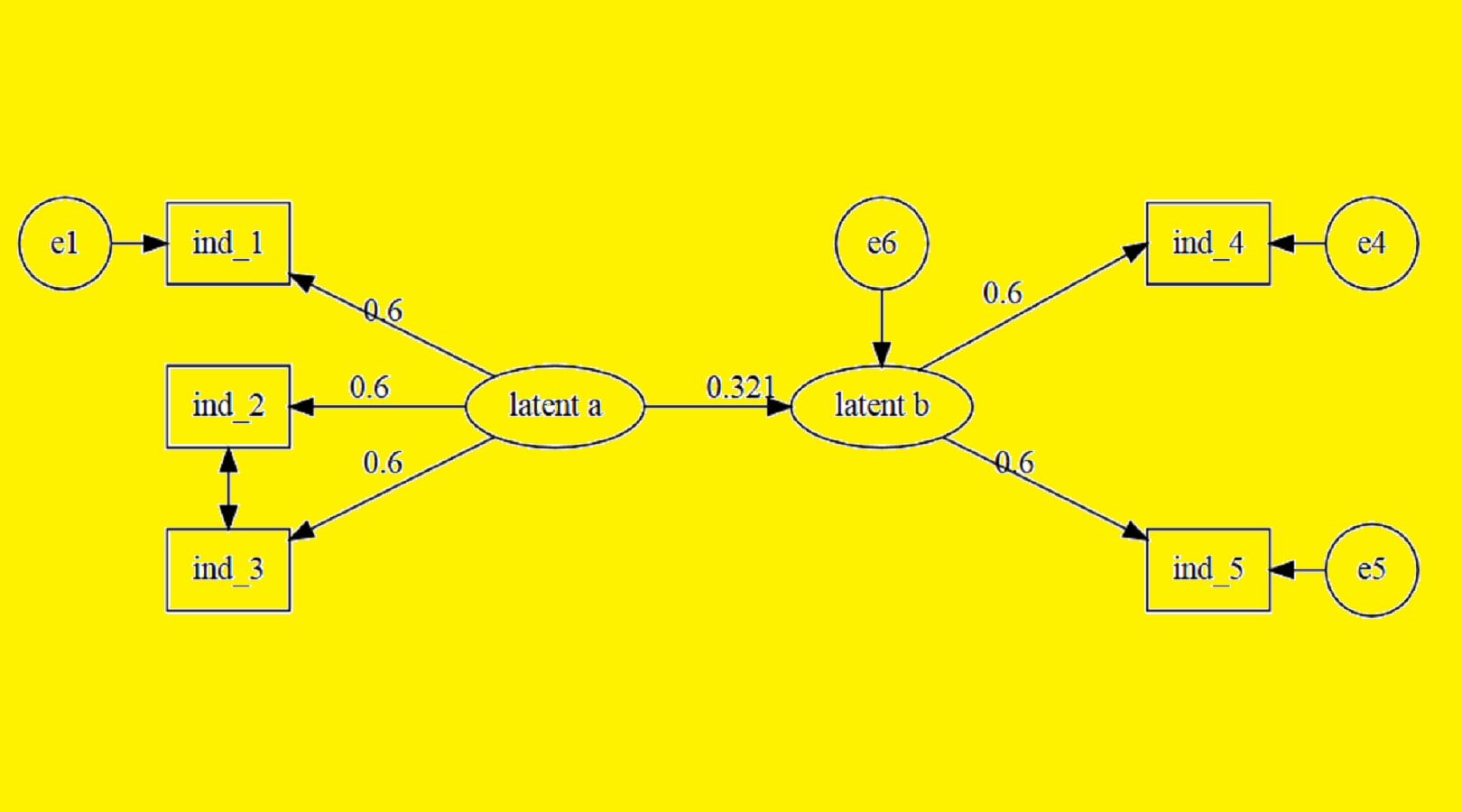
به بازار عرضه شده است. اين نرم افزار با استفاده از همبستگي و کوواريانس اندازه گيري شده، ميتواند مقادير بارهاي عاملي، واريانسها و خطاهاي متغيرهاي مکنون را برآورد يا استنباط کند و از آن ميتوان براي اجراي تحليل عاملي اکتشافي، تحليل عاملي مرتبه دوم، تحليل عاملي تاييدي و همچنين تحليل مسير (مدل يابي علت و معلولي با متغيرهاي مکنون) استفاده کرد.
تحلیل ساختاری کوواریانس که به آن روابط خطی ساختاری نیز می گویند، یکی از تکنیک های تحلیل مدل معادلات ساختاری است. جالب است بدانید که نام LISREL از عبارت
Linear Structural Relations
که به معنای روابط خطی ساختاری است، بدست آمده است.
5- تحليل عاملي اکتشافي (efa) و تحليل عاملي تاييدي (cfa)
تحليل عاملي ميتواند دو صورت اکتشافي و تاييدي داشته باشد. اينکه کدام يک از اين دو روش بايد در تحليل عاملي به کار رود مبتني بر هدف تحليل داده هاست.
تحليل عاملی اکتشافي
در تحليل عاملی اکتشافي(Exploratory factor analysis) پژوهشگر به دنبال بررسي دادههاي تجربي به منظور کشف و شناسايي شاخصها و نيز روابط بين آنهاست و اين کار را بدون تحميل هر گونه مدل معيني انجام ميدهد. به بيان ديگر تحليل عاملی اکتشافي علاوه بر آنکه ارزش تجسسي يا پيشنهادي دارد ميتواند ساختارساز، مدل ساز يا فرضيه ساز باشد.
تحليل اکتشافي وقتي به کار ميرود که پژوهشگر شواهد کافي قبلي و پيش تجربي براي تشکيل فرضيه درباره تعداد عاملهاي زيربنايي دادهها نداشته و به واقع مايل باشد درباره تعيين تعداد يا ماهيت عاملهايي که همپراشي بين متغيرها را توجيه ميکنند دادهها را بکاود. بنابر اين تحليل عاملی اکتشافي بيشتر به عنوان يک روش تدوين و توليد تئوري و نه يک روش آزمون تئوري در نظر گرفته ميشود.
تحليل عاملي اکتشافي روشي است که اغلب براي کشف و اندازه گيري منابع مکنون پراش و همپراش در اندازه گيريهاي مشاهده شده به کار ميرود. پژوهشگران به اين واقعيت پي برده اند که تحليل عاملي اکتشافي ميتواند در مراحل اوليه تجربه يا پرورش تستها کاملا مفيد باشد. توانشهاي ذهني نخستين ترستون، ساختار هوش گيلفورد نمونههاي خوبي براي اين مطلب ميباشد. اما هر چه دانش بيشتري درباره طبيعت اندازه گيريهاي رواني و اجتماعي به دست آيد ممکن است کمتر به عنوان يک ابزار مفيد به کار رود و حتي ممکن است بازدارنده نيز باشد.
از سوي ديگر بيشتر مطالعات ممکن است تا حدي هم اکتشافي و هم تاييدي باشند زيرا شامل متغير معلوم و تعدادي متغير مجهولاند. متغيرهاي معلوم را بايد با دقت زيادي انتخاب کرد تا حتي الامکان درباره متغيرهاي نامعلومي که استخراج ميشود اطلاعات بيشتري فراهمايد. مطلوب آن است که فرضيه اي که از طريق روشهاي تحليل اکتشافي تدوين ميشود از طريق قرار گرفتن در معرض روشهاي آماري دقيقتر تاييد يا رد شود. تحليل عاملی اکتشافي نيازمند نمونههايي با حجم بسيار زياد ميباشد.
تحليل عاملي تاييدي
در تحليل عاملي تاييدي (Confirmatory factor analysis) ، پژوهشگر به دنبال تهيه مدلي است که فرض ميشود دادههاي تجربي را بر پايه چند پارامتر نسبتا اندک، توصيف تبيين يا توجيه ميکند. اين مدل مبتني بر اطلاعات پيش تجربي درباره ساختار داده هاست که ميتواند به شکل:
1) يک تئوري يا فرضيه
2) يک طرح طبقه بندي کننده معين براي گويهها يا پاره تستها در انطباق با ويژگيهاي عيني شکل و محتوا
3)شرايط معلوم تجربي
و يا 4) دانش حاصل از مطالعات قبلي درباره دادههاي وسيع باشد.
تمايز مهم روشهاي تحليل اکتشافي و تاييدي در اين است که روش اکتشافي با صرفهترين روش تبيين واريانس مشترک زيربنايي يک ماتريس همبستگي را مشخص ميکند. در حالي که روشهاي تاييدي (آزمون فرضيه) تعيين ميکنند که دادهها با يک ساختار عاملي معين (که در فرضيه آمده) هماهنگ اند يا نه.
ضمنا خاطر نشان می شود برای دریافت ویدئوی آموزشی تحلیل عاملی تاییدی در نرم افزار لیزرل می توانید به این صفحه مراجعه نمایید:
درود بر شما کاربر محترم و بزرگوار، به عرض می رساند امروزه هزینه های نگهداری و ارتقای سایت بالا می باشد، لذا جهت ادامه فعالیت مجبور شدیم در بعضی از جاها تبلیغ بگذاریم.
لطفاً با کلیک بر روی لینک های زیر از ما حمایت کنید تا بتوانیم خدمات بهتری ارائه دهیم. مطمئن باشد هیچ مشکلی برای شما پیش نخواهد آمد.
با تشکر.
،
6- آزمونهاي برازندگي مدل کلي
با آنکه انواع گوناگون آزمونها که به گونه کلي شاخصهاي برازندگي(Fitting indexes) ناميده ميشوند پيوسته در حال مقايسه، توسعه و تکامل ميباشند اما هنوز درباره حتي يک آزمون بهينه نيز توافق همگاني وجود ندارد. نتيجه آن است که مقالههاي مختلف، شاخصهاي مختلفي را ارائه کرده اند و حتي نگارشهاي مشهور برنامههاي SEM مانند نرم افزارهاي lisrel, Amos, EQS نيز تعداد زيادي از شاخصهاي برازندگي به دست ميدهند.(هومن1384 ،235)
اين شاخصها به شيوههاي مختلفي طبقه بندي شده اند که يکي از عمدهترين آنها طبقه بندي به صورت مطلق، نسبي و تعديل يافته ميباشد. برخي از اين شاخص ها عبارتند از:
1-6- شاخصهاي GFI و AGFI
شاخص GFI – Goodness of fit index مقدار نسبي واريانسها و کوواريانسها را به گونه مشترک از طريق مدل ارزيابي ميکند. دامنه تغييرات GFI بين صفر و يک ميباشد. مقدار GFI بايد برابر يا بزرگتر از 0.09 باشد.
شاخص برازندگي ديگر Adjusted Goodness of Fit Index – AGFI يا همان مقدار تعديل يافته شاخص GFI براي درجه آزادي ميباشد. اين مشخصه معادل با کاربرد ميانگين مجذورات به جاي مجموع مجذورات در صورت و مخرج (1- GFI) است. مقدار اين شاخص نيز بين صفر و يک ميباشد. شاخصهاي GFI و AGFI را که جارزکاگ و سوربوم (1989) پيشنهاد کرده اند بستگي به حجم نمونه ندارد.
2-6- شاخص RMSEA
اين شاخص , ريشه ميانگين مجذورات تقريب ميباشد.
شاخص Root Mean Square Error of Approximation – RMSEA براي مدلهاي خوب برابر 0.05 يا کمتر است. مدلهايي که RMSEA آنها 0.1 باشد برازش ضعيفي دارند.
3-6- مجذور کاي
آزمون مجذور كاي (خي دو) اين فرضيه را مدل مورد نظر هماهنگ با الگوي همپراشي بين متغيرهاي مشاهده شده است را ميآزمايد، کميت خي دو بسيار به حجم نمونه وابسته ميباشد و نمونه بزرگ کميت خي دو را بيش از آنچه که بتوان آن را به غلط بودن مدل نسبت داد, افزايش ميدهد. (هومن.1384. 422).
4-6- شاخص NFI و CFI
شاخصNFI (که شاخص بنتلر-بونت هم ناميده ميشود) براي مقادير بالاي 0.09 قابل قبول و نشانه برازندگي مدل است. شاخص CFI بزرگتر از 0.09 قابل قبول و نشانه برازندگي مدل است. اين شاخص از طريق مقايسه يک مدل به اصطلاح مستقل که در آن بين متغيرها هيچ رابطه اي نيست با مدل پيشنهادي مورد نظر، مقدار بهبود را نيز ميآزمايد. شاخص CFI از لحاظ معنا مانند NFI است با اين تفاوت که براي حجم گروه نمونه جريمه ميدهد.
شاخصهاي ديگري نيز در خروجي نرم افزار ليزرل ديده ميشوند که برخي مثل AIC, CAIC ECVA براي تعيين برازندهترين مدل از ميان چند مدل مورد توجه قرار ميگيرند.
براي مثال مدلي که داراي کوچکترين AIC ,CAIC ,ECVA باشد برازندهتر است.(هومن1384 ،244-235) برخي از شاخصها نيز به شدت وابسته به حجم نمونه اند و در حجم نمونههاي بالا ميتوانند معنا داشته باشند.
برگرفته از سایت اطمینان شرق