آزمون کای دو(chi-square) یا خی دو چیست؟- نیکویی برازش و استقلال در SPSS

آزمون کای دو یا خی دو و یا مربع کای ازمونی است که فراوانی های مورد انتظار را با فراوانی های تحقیق مقایسه می کند تا مشخص شود آیا تفاوت معنا داری بین این دو فراوانی وجود دارد یا خیر. حال در ادامه ما دو نوع از آزمون کای دو را تعریف خواهیم کرد، سپس با مثالی ملموس آن را در SPSS اجرا خواهیم کرد.

آزمون کای دو (chi-square)چیست؟

دو نوع آزمون کای ۲ وجود دارد که هر کدام به منظوری متفاوت استفاده خواهند شد. در ادامه به این دو نوع خواهیم پرداخت.

آزمون کای دو برای نیکویی برازش

که برای تحلیل یک متغیر رده‌ای به کار می‌رود. به این صورت که اگر اختلافی در فراوانی میان رده‌های پاسخ وجود داشته باشد، آزمون کای دو برای نیکویی برازش آن را نشان می‌دهد. با توجه به نتایج این آزمون اگر مقدار معناداری آزمون برای گروهی کمتر از ۰/۰۵ به‌دست آمده باشد، می‌توان نتیجه گرفت که بین فراوانی‌های آن گروه تفاوت معناداری وجود دارد. به‌عبارتی تفاوت بین فراوانی‌ها از نظر آماری تایید می‌گردد.

آزمون کای دو برای استقلال

که برای تعیین رابطه‌ی بین دو متغیر رده‌ای از این آزمون کای دو استفاده می‌کنیم (جدول توافقی). به‌عبارتی اگر بخواهیم استقلال بین دو متغیر کیفی را آزمون کنیم از آماره کای دو دونمونه‌ای استفاده می‌کنیم. آماره کای دو بر مقادیر مشاهده شده و مورد انتظار که از طریق جدول توافقی به‌دست می‌آیند، استوار است. در جدول توافقی مقدار مشاهده شده عبارت است از تعدادی از نمونه‌ها که در یک خانه قرار دارند. مقدار مورد انتظار عبارت است از تعدادی که در صورت مستقل بودن دو متغیر پیش‌بینی می‌شود.

H_۰: دو متغیر کیفی مستقل هستند.

H_۱: دو متغیر کیفی مستقل نیستند.

جز اصلی جدول توافقی تعداد نمونه‌هایی است که در هر یک از خانه‌های جدول قرار می‌گیرند. روش‌های آماری که در این فرضیه‌های صفر به‌کار می‌روند بر اساس مقایسه موارد مشاهده شده در هر خانه با تعداد مورد انتظار آن عمل می‌کند. تعداد مورد انتظار به‌طور ساده تعدادی از نمونه‌هاست که در صورت صحیح بودن فرضیه صفر انتظار می‌رود در هر یک از خانه‌ها پیدا شود. فرضیه صفر در جدول توافقی به‌صورت مستقل بودن دو متغیر بیان می‌شود.

پیش‌فرض‌هایی که قبل از انجام این آزمون‌ها می‌بایستی برقرار باشند، به‌صورت زیرند:

نمونه‌گیری تصادفی: مشاهدات باید به‌طور تصادفی از جامعه انتخاب شوند.

استقلال مشاهدات: هر مشاهده مربوط به یک نفر است و هیچ شخصی دوبار در نمونه‌گیری حساب نمی‌شود.

اندازه فراوانی‌های مورد انتظار: زمانی که تعداد سلول‌ها کمتر از ۱۰ است و اندازه‌ی نمونه کوچک است، کمترین فراوانی مورد انتظاری که هر یک از سلول‌ها می‌بایستی برای آزمون کای دو داشته باشند ۵ است. با این حال، مقدار مشاهده شده می‌تواند کمتر از ۵ و یا حتی صفر باشد.

مثال آزمون کای دو یا خی دو برای نیکویی برازش

جدول زیر نگرش ۶۰ نفر را نسبت به ارتش آمریکایی مستقر در استرالیا نشان می‌دهد. اگر اختلافی در فراوانی میان رده‌های پاسخ وجود داشته باشد، آزمون کای دو برای نیکویی برازش آن را نشان می‌دهد.

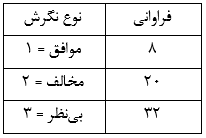
داده‌ها را در یک فایل SPSS ثبت کرده‌ایم، فایل داده‌ها را باز می‌کنیم:

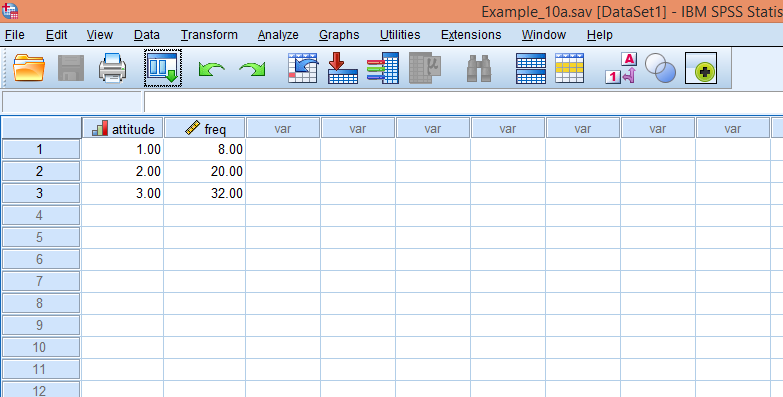
اکنون باید مقادیر ستون freq (فراوانی) را به عنوان وزن‌های متغیر attitude (نوع نگرش) تعریف کنیم. با این عمل مشخص می‌کنیم که 8 نفر کد 1 (موافق)، 20 نفر کد 2 (مخالف) و 32 نفر کد 3 (بی‌نظر) را انتخاب کرده‌اند. از منوی Data گزینه‌ی Weight Cases… را برگزینید تا کادر زیر باز شود:

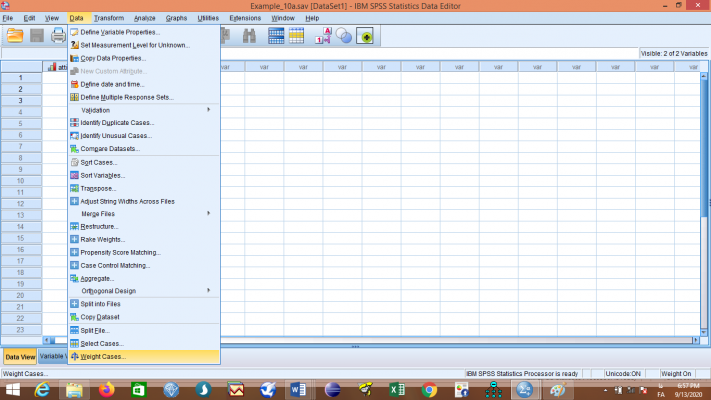
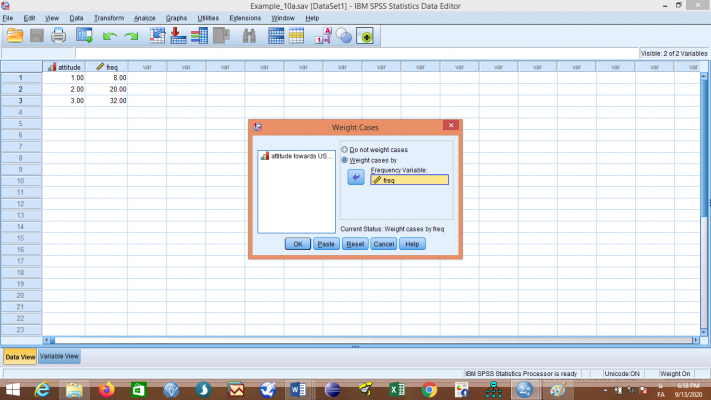
گزینه Weight cases by را انتخاب کنید و متغیر freq را به قسمت Frequency Variable انتقال دهید و روی گزینه OK کلیک کنید. با این عمل، وزن‌های مربوطه برای متغیر attitude تعریف می‌شوند.

اکنون از منوی Analyze به ترتیب گزینه‌های Nonparametric Tests، Legacy Dialogs و Chi-square… را انتخاب نمایید تا کادر مربوطه باز شود، متغیر attitude را به سمت راست منتقل و روی OK کلیک کنید.

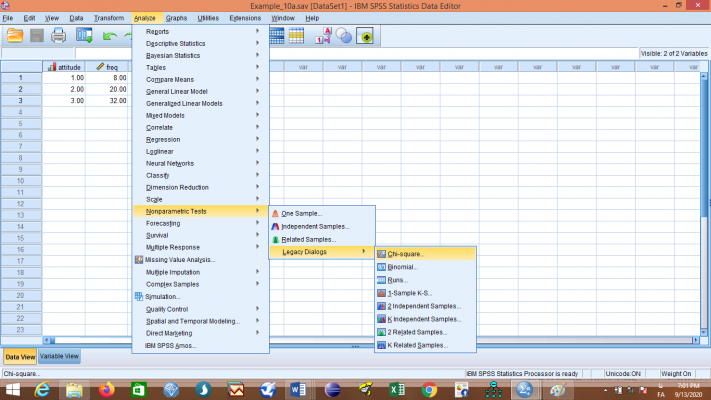
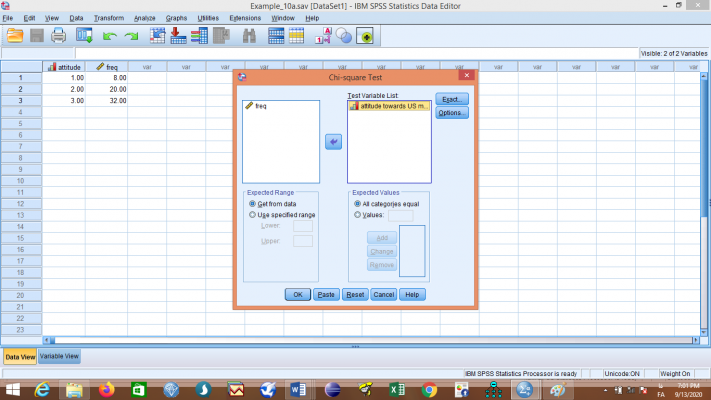
خروجی به صورت زیر می‌باشد:

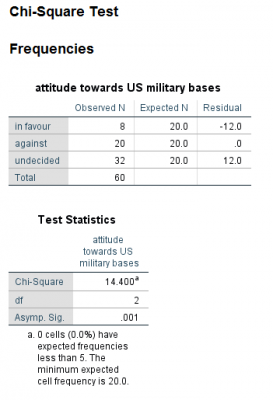
با توجه به جدول فوق آزمون کای دو معنادار است (چون Sig = 0.001 < 0.05)، بنابراین نتیجه می‌گیریم که اختلافی معنادار در فراوانی نگرش افراد، نسبت به ارتش مستقر در استرالیا وجود دارد. همچنین جدول فراوانی نشان می‌دهد که اکثر مردم بی‌نظر هستند.

در مثال فوق، فراوانی‌های مورد انتظار را برای هر یک از ۳ گروه، یکسان در نظر گرفتیم. یعنی به هر گروه فراوانی مورد انتظار ۲۰ را اختصاص دادیم یا به عبارت دیگر، شانس یک سوم را به هر گروه اختصاص دادیم. اکثر اوقات فراوانی‌های مورد انتظار در بین گروه‌ها به طور یکسان توزیع نمی‌شود. فرض کنید در مثال فوق به ترتیب فراوانی‌های مورد انتظار ۱۵، ۱۵ و ۳۰ را به گروه‌ها اختصاص دهیم، اکنون دوباره مثال را انجام می‌دهیم.

از منوی Analyze به ترتیب گزینه‌های Nonparametric Tests، Legacy Dialogs و Chi-square… را انتخاب نمایید تا کادر مربوطه باز شود، سپس متغیر attitude را به سمت راست منتقل کنید.

در قسمت Expected Values با انتخاب گزینه‌ی Values فیلد مقابل آن فعال می‌شود. در این قسمت عدد 15 را تایپ و روی Add کلیک کنید. دوباره 15 را تایپ و روی Add کلیک کنید. در پایان عدد 30 را تایپ و روی Add کلیک کنید، اکنون کادر باید همانند شکل زیر باشد:

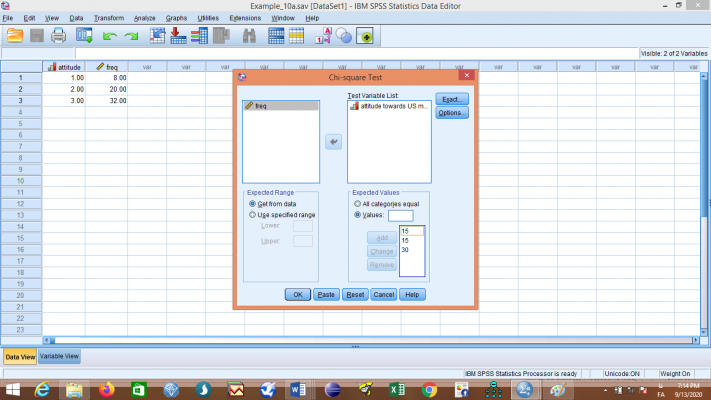
حال روی OK کلیک کنید تا خروجی نمایش یابد:

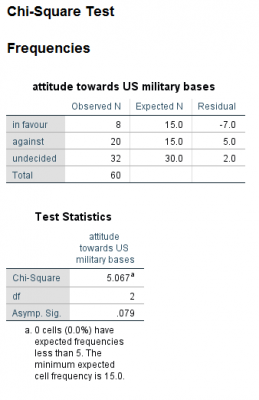
با توجه به آزمون کای دو مشاهده می‌کنیم که میان فراوانی‌های مشاهده شده (با توجه به فراوانی‌های موردانتظار و نسبت‌های داده شده به آن‌ها) اختلاف معناداری وجود ندارد (چون Sig = 0.079 > 0.05).

همان‌طور که قبلا هم اشاره کردیم هدف از ایجاد یک جدول توافقی، یافتن رابطه‌ی بین دو متغیر است، اکنون برای این منظور مثالی مطرح می‌کنیم:

مثال: (آزمون کای دو (ki2) برای استقلال)

فرض کنید می‌خواهیم بررسی کنیم که آیا سطح تحصیلات افراد از جنسیت مستقل است یا نه؟ نمونه‌ای متشکل از ۳۰۰ نفر برداشتیم و خلاصه نتایج را در جدول زیر آورده‌ایم:

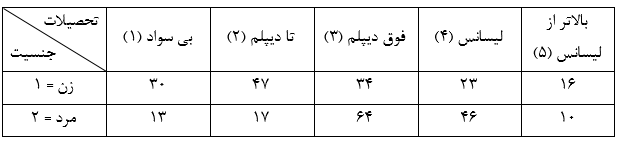
برای این‌که داده‌های جدول را در SPSS تعریف کنیم، ابتدا یک فایل داده جدید باز کنید و متغیرهای Gender و Education را به ترتیب با کدهای مربوطه تعریف نمایید. به علاوه لازم است متغیر دیگری به نام Count (یا هر نام دلخواه دیگری) ایجاد نمایید، این متغیر در بردارنده‌ی مقادیر موجود در جدول می‌باشد. پس از وارد کردن اطلاعات، فایل داده باید به صورت زیر باشد:

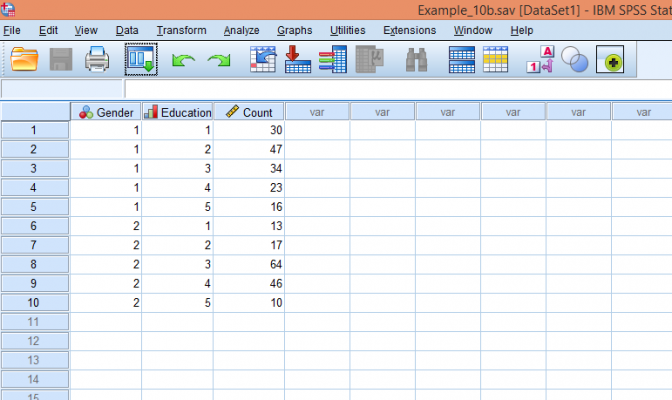
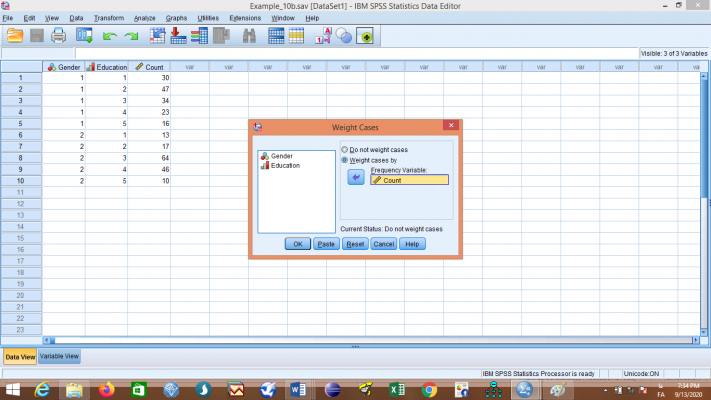
حال باید مقادیر ستون Count را به عنوان وزن‌های دو متغیر جنسیت و تحصیلات تعریف کنیم. از منوی Data گزینه‌ی Weight Cases… را برگزینید تا کادر زیر باز شود:

گزینه Weight cases by را انتخاب کنید و متغیر Count را به قسمت Frequency Variable انتقال دهید، سپس روی گزینه OK کلیک کنید. با این عمل، وزن‌های مربوطه برای متغیرها تعریف می‌شوند.

پس از تعریف متغیرها و تعیین وزن‌های مربوطه، به انجام تحلیل می‌پردازیم. از منوی Analyze به ترتیب گزینه‌های Descriptive Statistics و Crosstabs را انتخاب نمایید تا کادر مربوطه باز شود، متغیر Gender را به قسمت Row(s) و متغیر Education را به قسمت Column(s) انتقال دهید:

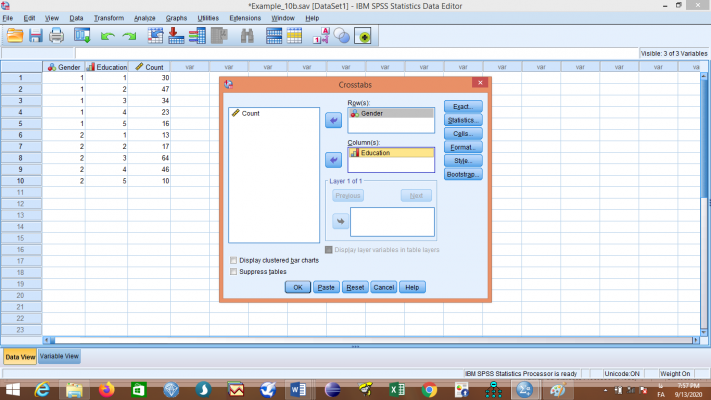
قبل از انجام تحلیل به بررسی گزینه‌های موجود در این کادر می‌پردازیم.

با کلیک روی دکمه Statistics کادر زیر نمایان می‌شود:

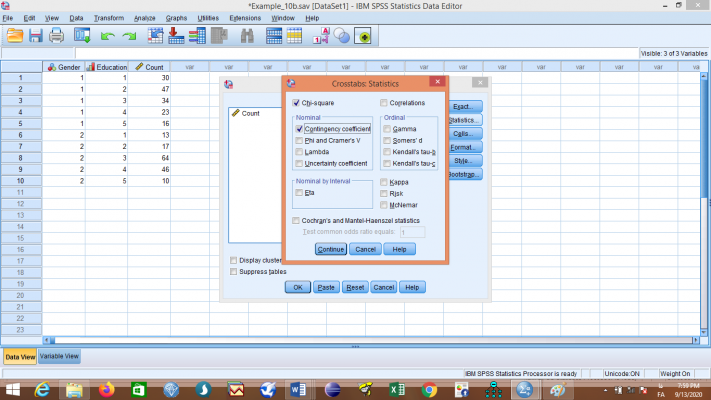
با توجه به نوع متغیر مورد مطالعه، آماره‌های مناسب در این جدول خلاصه شده‌اند. مثلا اگر هر دو متغیرمان اسمی و یا یکی اسمی و دیگری ترتیبی باشد، از آماره‌های قسمت Nominal استفاده می‌کنیم. اگر هر دو رتبه‌ای باشند، از آماره‌های قسمت Ordinal استفاده می‌کنیم و اگر یکی اسمی و دیگری فاصله‌ای باشد، از آماره Eta موجود در قسمت Nominal by Interval استفاده می‌کنیم.

مقدار شاخص‌های رابطه برای متغیرهای ترتیبی بین ۱- و ۱+ تغییر می‌کند؛ اما در متغیرهای اسمی، چون صحبت از جهت رابطه، معنا ندارد، مقدار این شاخص‌ها بین صفر تا ۱+ تغییر می‌کند. توجه کنید که استفاده از هر کدام از این آماره‌ها شرایط خاص خود را دارد که توضیحات مختصری از این شاخص‌ها را در جدول زیر آورده‌ایم:

آماره کای دو (Chi-square): توسط این آماره، تنها فرض مستقل بودن متغیرها را می‌توان بررسی کرد و مقدار همبستگی و رابطه را نمی‌تواند مشخص کند.

همبستگی (Correlation): از طریق این گزینه، دو نوع همبستگی محاسبه می‌شود. ضریب همبستگی پیرسون و ضریب همبستگی اسپیرمن. ضریب همبستگی پیرسون هنگامی که هر دو متغیر جدول کمّی (پیوسته) هستند، به کار می‌رود و مقدار آن بین 1- و 1+ تغییر می‌کند. مقدار صفر نشان می‌دهد که هیچ رابطه‌ی خطی بین متغیرها وجود ندارد.

برای جداولی که سطر و ستون آنها دربردارنده داده‌های رتبه‌ای است، ضریب همبستگی اسپیرمن را به کار می‌برند که همانند ضریب همبستگی پیرسون تفسیر می‌شود. زمانی که اندازه نمونه بزرگ باشد بهتر است از ضریب همبستگی اسپیرمن استفاده نشود؛ چون این ضریب برای نمونه‌های بزرگ به طور مجانبی استفاده می‌شود و از دقت لازم برخوردار نیست. از این رو از ضرایب همبستگی معادل همانند کندال استفاده می‌کنند.

ضریب توافق (Contingency Coefficient): این ضریب اندازه‌ای از همبستگی بر پایه‌ی آماره کای – دو ارائه می‌کند و مقادیر دامنه آن بین صفر و 1 می‌باشد. مقدار صفر بیان می‌کند که بین متغیرهای سطری و ستونی همبستگی وجود ندارد و مقادیر نزدیک به 1 نشان می‌دهند که درجه بالایی از همبستگی بین متغیرها وجود دارد. این ضریب برای جداول 2×2 و بالاتر به‌کار می‌رود.

ضریب فای و V‌ی کرامر (Phi and Cramer’s V): کاربرد ضریب فای تنها محدود به جداول 2×2 است. یعنی زمانی که هر یک از متغیرهای سطری و ستونی تنها ارزش‌های صفر (خیر) و یک (بلی) داشته ‌باشند. برای تعمیم این ضریب به جداول بزرگتر از آماره V کرامر استفاده می‌کنیم.

ضریب لاندا (Lambda): این ضریب در دو حالت محاسبه می‌شود:

• نامتقارن: به این دلیل به آن نامتقارن گویند که در محاسبه‌ی آن بسته به این که کدام یک از دو متغیر را مستقل و کدام را وابسته در نظر بگیریم، مقدار لاندا تغییر می‌کند؛ یعنی قرینه نیست.
• متقارن: در این حالت فرقی نمی‌کند کدام یک از متغیرها را مستقل و کدام را وابسته در نظر بگیریم. در هر دو صورت مقدار لاندا یکسان خواهد بود.

در هنگام استفاده از این ضریب می‌بایستی مراقب بود. زمانی که دو متغیر از نظر آماری مستقل هستند، مقدار لاندای آن‌ها صفر خواهد بود؛ ولی عکس آن صحیح نیست. یعنی صفر بودن لاندا لزوما به معنای مستقل بودن نیست. به عبارت دیگر ممکن است دو متغیر با هم رابطه داشته باشند، اما لاندای آن‌ها صفر باشد، زیرا دانستن متغیر مستقل، هیچ کمکی به پیش‌بینی ما نکرده است.

گاما (Gamma): این آماره اندازه‌ای متقارن (یعنی فرقی نمی‌کند کدام متغیر مستقل و کدام وابسته باشد) از رابطه‌ی بین دو متغیر ترتیبی است که دامنه‌ی آن بین 1- و 1+ تغییر می‌کند. مقدار نزدیک به 1 از نظر قدر مطلق، نمایانگر یک پیوند قوی بین دو متغیر می‌باشد؛ مقدار نزدیک به صفر، بیان کننده‌ی یک رابطه‌ی ضعیف است.

d سامرز (Sommers`d): این ضریب همانند شاخص گاماست؛ ولی در آن یکی از متغیرها مستقل و دیگری وابسته فرض می‌شود و دامنه آن بین 1- و 1+ تغییر می‌کند.

تاو – b کندال (Kendall`s tau-b): این شاخص برای زمانی مناسب است که جدول توافقی شما مربع است و دامنه‌ی آن بین 1- و 1+ تغییر می‌کند.

تاو – c کندال (Kendall`s tau-c): این شاخص برای جداول مختلف قابل استفاده است و مقدار آن بین 1- و 1+ متغیر است.

ضریب اتا (Eta): این شاخص برای متغیرهای اسمی و فاصله‌ای به‌کار می‌رود، که در آن متغیر وابسته بر حسب مقیاس فاصله‌ای و متغیر مستقل بر حسب مقیاس اسمی اندازه‌گیری شده‌اند. دامنه‌ی این شاخص بین صفر تا 1 است. این شاخص نامتقارن، هیچ رابطه‌ی خطی بین متغیرها در نظر نمی‌گیرد. مقدار صفر این کمیت بیان می‌کند که هیچ رابطه‌ای بین متغیرهای سطری و ستونی وجود ندارد و مقادیر نزدیک به 1 بیان می‌کند، بین آن‌ها یک رابطه با درجه بالا وجود دارد. در خروجی SPSS دو مقدار برای این ضریب نمایش می‌یابد که هر بار یکی از متغیرهای سطری یا ستونی را به عنوان متغیر فاصله‌ای (وابسته) در نظر می‌گیرد.

کاپا (Kappa): ضریب کاپا، میزان توافق دو فرد رتبه‌دهنده که یک متغیر را رده‌بندی کرده‌اند، نشان می‌دهد. مثلا از دو معلم می‌خواهیم نمرات دانش‌آموزان را در یک مقیاس سه نمره‌ای درجه‌بندی کنند، می‌خواهیم بدانیم که این دو فرد چقدر با هم توافق دارند و درجه‌بندی‌هایشان به هم نزدیک است. مقدار 1 این ضریب بیانگر توافق کامل و مقدار صفر نشان‌دهنده‌ی تصادفی بودن توزیع کدهاست. نکته‌ای که در هنگام استفاده از این ضریب باید بدان توجه داشته باشید این است که هر دو متغیر از مقادیر رده‌بندی (کدهای) یکسانی استفاده کنند و دارای تعداد یکسانی رده باشند.

ریسک (Risk): اندازه‌ای از میزان رابطه بین یک فاکتور (متغیر گروه‌بندی شده) و رخ دادن یک پیشامد (یک گزینه پاسخ) می‌باشد و برای جداول 2×2 به‌کار می‌رود. اگر فاصله اطمینان این آماره عدد 1 را دربرداشته باشد، نشان‌دهنده این است که فاکتور با پیشامد رابطه ندارد.

مک نمار (McNemar): اگر متغیرهای دو حالتی جفت داشته باشیم، از این آماره استفاده می‌کنیم. متغیر دو حالتی متغیری است که تنها دارای مقادیر صفر و 1 است و جفت بدان معنی است که پاسخ‌های هر دو متغیر برای یک گروه از افراد به‌دست آمده‌اند، همانند اندازه‌گیری ضربان قلب، قبل و بعد از تمرین. از این آماره برای آشکارسازی تغییرات در پاسخ‌ها به دلیل انجام یک عمل (قبل و بعد) استفاده می‌کنیم.

آماره کاکران و مانتل – هنزل (Cochran`s and Mantel Hanszel Statistics): از این آماره برای آزمون استقلال بین یک متغیر فاکتور دوحالتی و یک متغیر پاسخ دوحالتی شرطی شده روی ساختارهای متغیرهای تصادفی کمکی (که به وسیله متغیرهایی که در قسمت Layer تعریف می‌کنیم، مشخص می‌شوند) استفاده می‌شود. توجه کنید که اگر یک متغیر Layer تعریف کنیم، آماره‌های دیگر به صورت لایه به لایه محاسبه می‌شوند؛ ولی این آماره یک‌بار برای تمام لایه‌ها محاسبه می‌شود.

دوباره به مثال بازمی‌گردیم، گزینه‌های Chi-square و Contingency Coefficient را انتخاب و روی Continue کلیک کنید تا به کادر قبل بازگردید. در این کادر روی OK کلیک نمایید تا خروجی محاسبه شود:

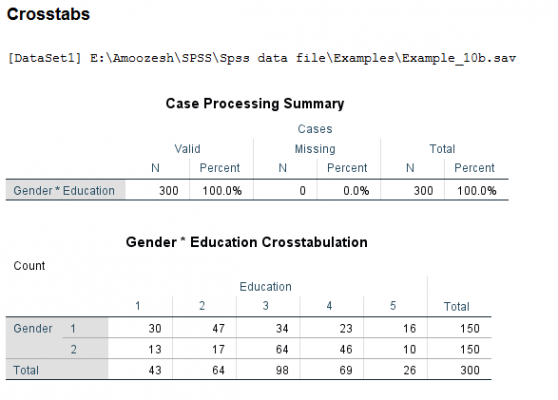
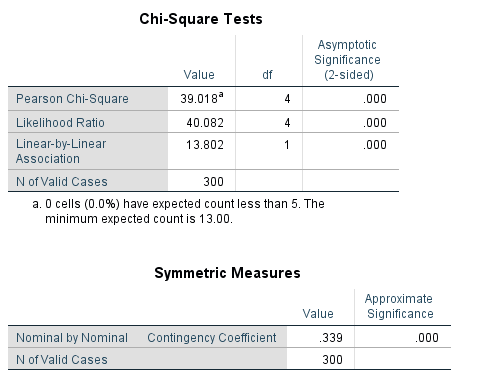
در مورد دو جدول اول قبلا توضیح داده‌ایم. در سومین جدول با عنوان Chi-square Tests مقدار آماره کای – دو 018/39 گزارش شده است و مقدار معناداری مرتبط با آن Sig = 0.000 است؛ یعنی فرض استقلال متغیرهای جنسیت و سطح تحصیلات رد می‌شود. از طریق چهارمین جدول با توجه به مقدار ضریب توافق یعنی، 339/0 درمی‌یابیم که نسبت پایینی از همبستگی بین این متغیرها وجود دارد.

نکته: زمانی که فراوانی‌های مورد انتظار خانه‌های جدول کوچک باشند (کمتر از ۵) برای انجام آزمون استقلال، نمی‌توان از آزمون کای دو یا خی دو استفاده نمود بنابراین باید از آزمون‌های معادل یا آزمون دقیق فیشر استفاده کرد، مخصوصا هنگامی که جدول ۲×۲ است.

برگرفته از : آمار پیشرو