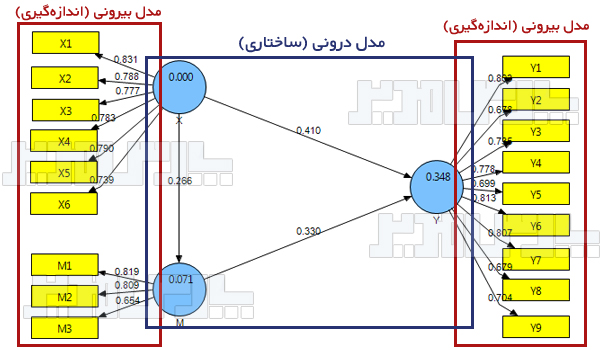
روایی واگرا (تشخیصی)
روایی واگرا Discriminant validity معیاری است که نشان میدهد چقدر سنجههای عوامل متفاوت واقعا باهم تفاوت دارند. در یک پرسشنامه برای سنجش عوامل مختلف سوالات متعددی مطرح میشود بنابراین لازم است که مشخص شود این سوالات از یکدیگر متمایز بوده و باهم همپوشانی ندارند.
این معیار در برابر روایی همگرا یا Convergent validity قرار میگیرد و گاهی به عنوان Divergent validity نیز در مقالههای علمی از آن یاد میشود. روایی همگرا به همبستگی سوالات یک سازه باهم اشاره دارد و روایی واگرا بر عدم همبستگی بین سوالات یک سازه با سوالات سازه دیگر دلالت دارد.
یکی از مهمترین مسائل در پژوهشها، تعیین میزان روایی و پایایی ابزار گردآوری دادههای پژوهش است. در بخش اعتبار یا روایی پرسشنامه Reliability، پژوهشگر در پی آن است که مشخص سازد آیا یافتههای بدست آمده از پژوهش را میتوان به کل جامعه یا گروههای مشابه آن تعمیم داد یا خیر؟ برخلاف پایایی یا اعتماد که مسئلهایی کمی است و اندازهگیری آن سادهتر است اعتبار پرسشنامه، مسألهای کیفی است و اندازهگیری و ارزیابی آن مشکلتر است. روایی به این سوال پاسخ میدهد که ابزار اندازهگیری تا چه حد خصیصه مورد نظر را میسنجد.
در نرم افزار Smart PLS و تکنیک حداقل مربعات جزیی سه روش برای محاسبه روایی وجود دارد:
- روایی سازه
- روایی همگرا
- روایی واگرا
تعریف روایی واگرا
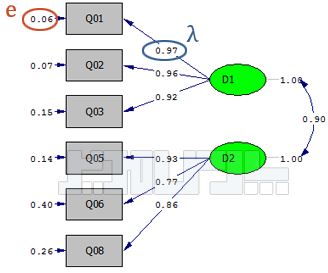
روایی واگرا نشان میدهد چقدر سوالات یک عامل با سوالات سایر عوامل تفاوت دارند. این معیار یکی از معیارهای اصلی برازش مدلهای اندازهگیری در روش PLS است و براساس بارهای عاملی مربوط به گویههای هر سازه تعیین میشود. روایی واگرا بر همبستگی پایین سنجههای یک متغیر پنهان با یک متغیر غیر مرتبط با آن (از نظر پژوهشگر) اشاره دارد. این معیار در روش حداقل مربعات جزئی از دو طریق سنجیده میشود. یکی روش بارهای عاملی متقابل است که میزان همبستگی بین شاخصهای یک سازه را با همبستگی آنها با سازههای دیگر مقایسه میکند و روش دیگر معیار پیشنهادی فورنل و لارکر Fornell & Larcker است که در این پژوهش مورد استفاده قرار گرفته است.
کلاس فورنل و دیوید لارکر
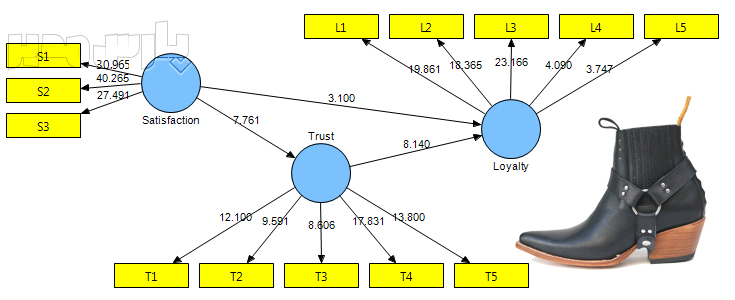
روایی واگرا یا در برابر روایی همگرا validity قرار دارد. فورنل و لارکر (۱۹۸۱) بیان کردند روایی واگرا وقتی در سطح قابل قبول است که میزان AVE برای هر سازه بیشتر از واریانس اشتراکی بین آن سازه و سازههای دیگر (یعنی مربع مقدار ضرایب همبستگی بین سازهها) در مدل باشد. بر این اساس روایی واگرای قابل قبول یک مدل اندازهگیری حاکی از آن است که یک سازه در مدل تعامل بیشتری با شاخصهای خود دارد تا با سازههای دیگر. در روش حداقل مربعات جزئی و مدلیابی معادلات ساختاری، این امر به وسیله یک ماتریس صورت میگیرد که خانههای این ماتریس حاوی مقادیر ضرایب همبستگی بین سازهها و قطر اصلی ماتریس جذر مقادیر AVE مربوط به هر سازه است.
در نرم افزار Smart PLS از قسمت Latent Variable Correlations در فایل خروجی استفاده میشود. قطر اصلی هم از مجذور AVE استفاده میشود.
روایی تشخیصی چیست؟
منظور از روایی تشخیصی همان روایی واگرا است. در زبان لاتین از دو اصطلاح Discriminant validity و Divergent validity استفاده میشود. این اصطلاح هر دو معادل هم استفاده میشوند و در مقالههای مختلف به جای هم به کار میروند. در زبان فارسی واژه Discriminant به معنای مشخصکننده یا تفکیک کننده ترجمه میشود. واژه Divergent نیز به صورت منشعب یا واگرا ترجمه میشود. بنابراین هر دو اصطلاح یکسان هستند و روایی تشخیصی چیز جدیدی نیست.
سه نگردد بریشم ار او را —– پرنیان خوانی و حریر و پرند
اگر به ابریشم بگویید پرند، پرنیان و حریر بازهم همان ابریشم است.
روایی واگرای یگانه-دوگانه HTMT
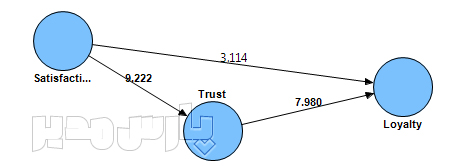
معیار Heterotrait-Monotrait Ratio یا شاخص HTMT در کانون تحلیل آماری پارس مدیر با عنوان معیار روایی یگانه-دوگانه ترجمه شده است. این معیار توسط هنسلر و همکاران (۲۰۱۵) برای ارزیابی روایی گرا ارائه شده است. معیار HTMT جایگزین روش قدیمی فورنل-لارکر شده است. حد مجاز معیار HTMT میزان ۰/۸۵ تا ۰/۹ میباشد. اگر مقادیر این معیار کمتر از ۰/۹ باشد روایی واگرا قابل قبول است. امکان محاسبه شاخص HTMT در نرم افزار Smart PLS 3 وجود دارد. برای این منظور باید رویه بوتاستراپینگ کامل را اجرا کنید.
برگرفته از پارس مدیر – نویسنده آرش حبیبی
دانلود کتاب آموزش تصویری تعیین حجم نمونه با Spss sample power نرم افزار