حداقل مربعات جزئی PLS

آموزش حداقل مربعات جزئی : Partial Least Squares, PLS

حداقل مربعات جزئی یا Partial Least Squares یک روش ناپارامتریک است که جانشین مناسبی برای مدل معادلات ساختاری می‌باشد. روش حداقل مربعات جزئی به حجم نمونه حساسیت کمتری دارد و نیازی به نرمال بودن داده‌ها ندارد. بنابراین در موارد زیر جانشین مدلسازی معادلات ساختاری می‌شود:

• زمانیکه حجم نمونه کوچک باشد
• زمانیکه داده‌ها نرمال نباشد

دقت کنید اگر داده‌ها نرمال باشد یا نمونه بزرگ باشد هم می‌توان از حداقل مجذورات جزیی استفاده کرد.

نرم افزارهای متعددی برای حداقل مجذورات جزئی وجود دارد که مهمترین آنها عبارتند از:

• نرم افزار Visual PLS
• نرم افزار Smart PLS

یکی از عمده‌ترین دلایل گرایش دانشجویان به استفاده از تکنیک حداقل مربعات جزئی این است که این تکنیک به فرض نرمال بودن جامعه و همچنین حجم نمونه متکی نیست. این در حالی است که برای انجام تکنیک معادلات ساختاری و نرم‌افزار لیزرل به حجم انبوهی از داده‌ها نیاز است. برای حل مسائل حداقل مربعات جزئی یا PLS می‌توانید از نرم افزار SmartPLS استفاده کنید. نرم افزار smartpls یک نرم افزار رایگان است که دریافت آن کمی دردسر دارد ولی در وب سایت پارس‌ مدیر نحوه دانلود آن تشریح شده است.

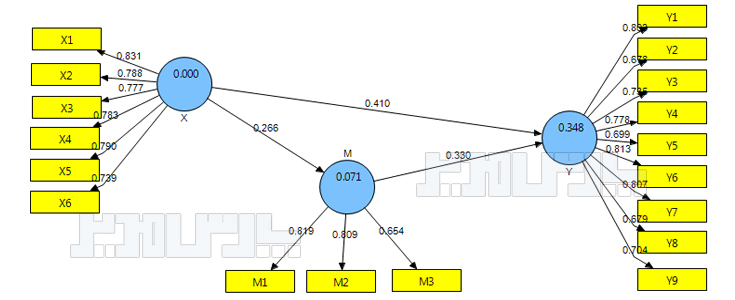
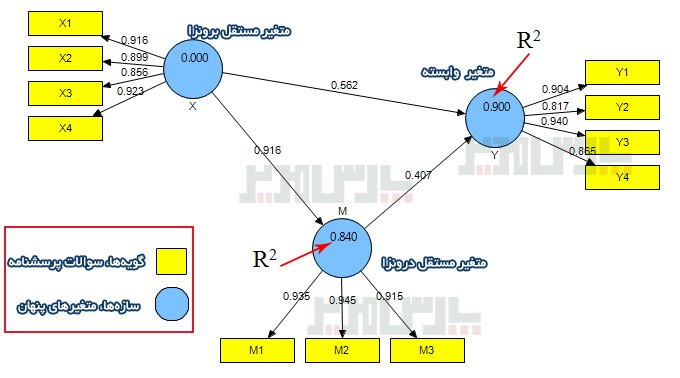
طراحی مدل حداقل مربعات جزیی

مانند مدل معادلات ساختاری در اینجا نیز باید با دو مفهوم متغیر پنهان و متغیر مشاهده پذیر آشنا باشد. متغیرهای پنهان همان عامل‌های اصلی یا سازه‌ها هستند که در شکل زیر با دایره نمایش داده شده اند. این متغیرها می‌توانند مستقل یا وابسته باشند. متغیرهای مشاهده پذیر همان گویه‌ها یا سوالات پرسشنامه هستند که در شکل زیر با مستطیل نمایش داده شده اند.

ساختار مدل حداقل مجذورات جزیی

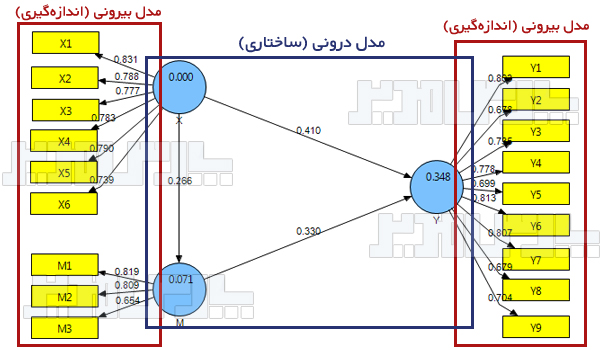
مدل درونی و مدل بیرونی

مدل حداقل مجذورات جزئی به دو دو مدل بیرونی و مدل درونی قابل تفکیک است.

مدل بیرونی : مدل بیرونی یا Outer Model روابط گویه‌ها (سوالات پرسشنامه) با عامل‌ها (متغیرهای پنهان) را نشان می‌دهد و معادل تحلیل عاملی تاییدی یا مدل اندازه‌گیری در نرم افزار لیزرل و اموس می‌باشد.

مدل درونی : مدل درونی یا Inner Model مشابه تحلیل مسیر و بخش ساختاری یک مدل معادلات ساختاری است. پس از آزمون مدل بیرونی لازم است تا مدل درونی که نشانگر ارتباط بین متغیرهای پنهان است، ارایه شود. با استفاده از مدل درونی می‌توان به بررسی فرضیه‌های پژوهش مدل پرداخت.

مدل درونی و مدل بیرونی

تفسیر مدل حداقل مربعات جزئی

برای شناسایی قدرت و جهت روابط میان عناصر از تخمین استاندارد استفاده می‌شود. این مقادیر که در شکل فوق نیز قابل مشاهده است باید بالای ۰/۳ باشند. هرچه میزان بارعاملی بیشتر باشد قدرت روابط بیشتر است.

برای بررسی معناداری باید آماره t برآورد شود. برای این منظور از خودگردان سازی (بوت استراپینگ) یا برش جک-نایف استفاده می‌شود. اگر مقادیر آماره تی بالای ۱/۹۶ باشد رابطه معنادار است.

شاخص‌های برازش مدل

در تکنیک حداقل مجذورات جزئی بر خلاف مدل معادلات ساختاری شاخص‌های زیادی برای برازش وجود ندارد.

عمده ترین شاخص‌های برازش مدل اندازه‌گیری عبارتند از:

• روایی همگرا
• روایی واگرا
• شاخص HTMT
• پایایی ترکیبی

عمده ترین شاخص‌های برازش مدل ساختاری عبارتند از:

• ضریب تشخیص R²
• شاخص GOF
• شاخص بلایندفولدینگ Q²
• شاخص اندازه اثر F²

برای مطالعه بیشتر به بحث شاخص‌های برازش حداقل مربعات جزئی رجوع کنید.

حجم نمونه حداقل مربعات جزئی

بحث تعیین حجم نمونه PLS یکی از مباحث مهم حداقل مجذورات جزئی است. حوزه دیگری که در آن مدلسازی معادلات ساختاری مبتنی بر کوواریانس پیشنهاد می‌شود، شرایطی است که در آن سایز نمونه کوچک است، برای این رویکرد حداقل سایز نمونه باید ۱۰۰ باشد (بدون توجه به خصوصیات سایر داده ها) تا بتوان از راهکارهای مشکل ساز پرهیز کرد و به سطح پذیرش قابل قبولی دست یافت. حتی بسیاری از پژوهشگران، حداقل سایز نمونه را ۲۰۰ پیشنهاد می‌کنند تا از نتایجی که قابل تفسیر نیستند( مانند واریانس منفی و یا همبستگی بالای ۱) پرهیز شود.

حداقل مربعات جزئی در شرایطی که نمونه بسیار کوچک است نیز می‌تواند مورد استفاده قرار بگیرد. اگرچه این گونه شرایط فقط برای تحلیل قدرت آماری می‌تواند بکار برده شود. مونت کارلو نشان داد که این رویکرد می‌تواند برای حجم نمونه کمتر از ۵۰ نیز بکار رود، اچ. ولد با استفاده از ۲۷ متغیر، دو سازه پنهان و مجموعه داده هایی متشکل از ۱۰ نمونه دست به تحلیل زد. با این حال با در نظر گرفتن مشکل پایداری در مقیاس بزرگ، هنوز این مدل با محدودیت هایی روبروست.

جمع بندی بحث حداقل مربعات جزئی

حداقل مربعات جزئی راهکاری برای آزمون فرضیه‌ها است و زمانی بکار میرود که حجم نمونه محدود باشد یا داده‌ها نرمال نباشند. بدون اینکه فرض هایی مانند فرضهای توزیع، و یا مقیاسهای اسمی، ترتیبی، و فاصلهای برای متغیرها، وجود داشته باشند، نتایج کار قابل استفاده میباشد. البته باید این نکته را نیز در ذهن داشت که حداقل مربعات جزئی هم همانند تمامی تکنیکهای آماری، نیازمند فرضهای خاصی است. مهمترین فرضیه، تشخیص “پیش‌بینی کننده” است. این الزام عنوان میکند که باید بخش سیستماتیک رگرسیون خطی را از روی انتظارات موقعیتی از متغیر وابسته تعریف کرد تا بتوان بر اساس رگرسیون نتیجه‌گیری کرد. با این حال، مشکل ثبات و پایداری در مقیاس بزرگ همچنان وجود دارد.

با توجه به مشکل سازگاری در نمونه‌های بزرگ، میتوان در مورد مناسب بودن حداقل مربعات جزئی دچار تردید شد و پرسید که چرا این تکنیک نمی‌تواند یکی از خصوصیت‌های کلیدی یک مدل آماری (پایداری برآوردکننده ) را تضمین کند. پاسخ این است که این رویکرد با اصول خودش وارد وضعیتهای مختلف می‌شود .هدف از مدلسازی معادلات ساختاری مبتنی بر کوواریانس، تعیین ماتریس پارامترهای مدل Φ است که ماتریس کوواریانس پیش‌بینی شده توسط مدل نظری Σ(Φ)احتمال بسیار نزدیکی به ماتریس کوواریانس نمونه S دارد. برای این منظور باید تابع F(S, Σ) تعریف شود. وقتی S=Σ است، این تابع ارزش صفر را به خود اختصاص می‌دهد سایر موارد که ارزش تابع مثبت است، تفاوت بین Σ و S افزایش مییابد. با توجه به اینکه ماتریس کوواریانس نمونه، مبتنی بر احتمال شاخص اندازهگیری شده است، تابعی که بسیار در این خصوص استفاده می‌شود، تابع حداکثر کردن نرمال نظری است.

برگرفته از پارس مدیر – نویسنده آرش حبیبی