تحلیل مسیر

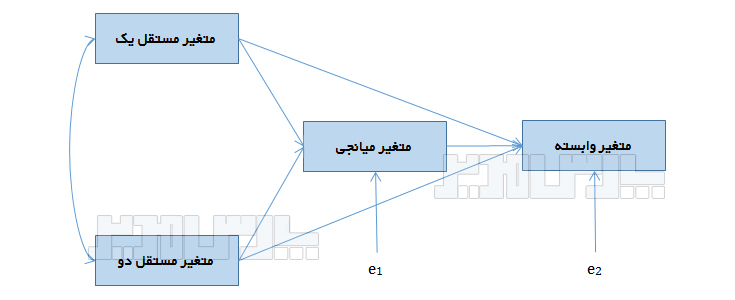
تحلیل مسیر (path analysis) روشی آماری مبتنی بر تحلیل رگرسیون چند متغیرى است که برای سنجش روابط متغیرها در یک مدل علّی استفاده می‌شود. در این روش از ضریب بتای استاندارد رگرسیون جهت تعیین جهت و شدت روابط میان متغیرها استفاده می‌شود. مقدار آماره تی نیز معناداری روابط را نشان می‌دهد.

هدف تحلیل مسیر به دست آوردن برآوردهاى کمى روابط على ( همکنشی یکجانبه یا کواریته) بین مجموعه اى از متغیرهاست. ساختن یک مدل علی لزوماً به معنای وجود روابط علی در بین متغیرهای مدل نیست بلکه این علیت بر اساس مفروضات همبستگی و نظر و پیشینه تحقیق استوار است. برای انجام محاسبات مربوط به تحلیل مسیر می‌توان از نرم‌افزار SPSS استفاده کرد.

تحلیل مسیر جهت و شدت روابط متغیرهای تحقیق را نشان می‌دهد. مقادیری که جهت و میزان تاثیر میان متغیرها را نشان می‌دهند ضریب مسیر نامیده می‌شوند و با به صورت قراردادی با حرف بتای لاتین β نمایش داده می‌شوند. ضرایب مسیر همان ضریب استاندارد شده رگرسیون هستند. بنابراین برای تحلیل مسیر باید از رگرسیون خطی ساده استفاده شود. تحلیل مسیر تنها بر روی متغیرهای قابل مشاهده انجام پذیر است و اگر بخواهید بین ابعاد تحلیل مسیر را اجرا کنید باید میانگین سوالات هر بعد را حساب کنید تا متغیر پنهان به یک متغیر قابل مشاهده تبدیل شود.

پیش‌فرض‌های تحلیل مسیر

برای انجام این محاسبات باید پیش‌فرض‌هایی در نظر گرفته شود که مهم‌ترین آنها عبارتند از:

• به ازای هر متغیر در مدل بین ۱۰ تا ۲۰ نمونه لازم است.
• از متغیرهای نسبی و فاصله‌ای استفاده شود.
• وجود رابطه خطی بین متغیرهای پیش بین با متغیر وابسته (Residual plot in regression Scatterplots)
• استقلال خطاها یا غیر همبسته بودن جملات خطای متغیرها (آزمون دوربین-واتسون)
• نرمال بودن داده‌ها و مشخص کردن آن با آزمون (Komogorov-Smirnov statistic)
• عدم وجود همخطی چندگانه (Multicollinearity)
• هم‌خطی بودن چندگانه زمان بروز می‌یابد که بین حداقل دو متغیر مستقل همبستگی بالایی وجود داشته باشد.
• یک سویه بودن جهت مدل (Recursive)

منظور از یک سیوه بودن این است که اگر A بر B تاثیر داشته باشد و B بر C اثر داشته باشد C بر A نمی تواند تاثیر داشته باشد. همچنین در بیشتر مطالعه مدیریت و علوم اجتماعی از طیف لیکرت استفاده می‌شود. این مقیاس رتبه‌ای است لیکن بسیاری از پژوهشگران با کمی تسامح مقیاس لیکرت را مقیاس فاصله‌ای در نظر می‌گیرند.

اصول ترسیم نمودار مسیر

۱- عدم وجود حلقه

۲- عدم وجود مسیر رفت و برگشت بین متغیرها

۳- حداکثر تعداد همبستگی‌های مجاز بین متغیرهای درونزا برابر با تعداد مسیرها

خطاهای ترسیم مدل در تحلیل مسیر

متغیر‌های درونزا و برونزا

متغیرهای یک مدل می‌توانند درون‌زا (Endogenous) یا برون‌زا (Exogenous) باشند بنابراین سه نوع متغیر قابل تمایز است:

متغیر مستقل برونزا : متغیری که از هیچ متغیر دیگری تاثیر نمی گیرد اما بر همه یا برخی متغیرهای مدل تاثیر دارد. مقدار متغیر برونزا توسط سایر متغیرهای درون مدل تعیین نمی شود بلکه مقدار آن درخارج مدل تعیین می‌شود. متغیر برونزا متغیری است که هیچ اثری از سایر متغیرهای الگو و مدل طراحی شده نمی پذیرد.

متغیر مستقل درونزا (میانجی) : متغیری که از برخی متغیرها تاثیر می‌گیرد و برخی متغیرها تاثیر می‌گذارد.

متغیر وابسته : متغیری است که بر هیچ متغیری تاثیری ندارد اما از همه یا برخی متغیرهای مدل تاثیر می‌پذیرد.

از نظر نموداری متغیر برونزا متغیری است که هیچ فلشی به آن وارد نمی شود در حالیکه متغیر درونزا متغیری است که حداقل یک فلش به آن وارد می‌شود.

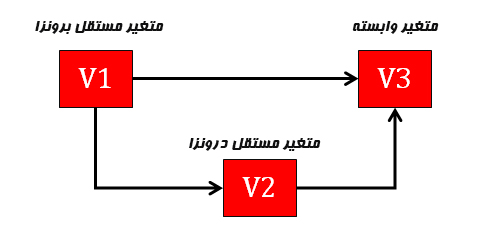
متغیر‌های درونزا و برونزا

مسیر

مسیر در مدل علّی نشان دهنده اثر یک متغیر بر متغیر دیگر است. در تحلیل مسیر معمولا مسیر را با یک فلش جهت دار یک طرفه که ازمتغیر برونزا به متغیر مربوطه درونزا رسم شده است نمایش می‌دهند. میزان تاثیر متغیر i بر متغیر j با نماد β_ij نمایش داده می‌شود. اگر این مقدار منفی باشد یعنی رابطه معکوس است و اگر مثبت باشد این رابطه مستقیم است. مقدار ضریب بتا بین [۱ و ۱-] است و هر چه قدر مطلق این مقدار از ۰/۳ بیشتر باشد نشان می‌دهد تاثیر قوی تر است. اگر مقدار آماره t از ۱/۹۶ بزرگتر باشد رابطه معنادار است.

جملات خطا

جمله خطا یا error term نشان دهنده میزانی از واریانس متغیر درونزا است که از سوی متغیرهای موثر بر آن تبیین می‌گردد. بنابر این در یک مدل علّی به تعداد متغیرهای درونزا، جمله خطا وجود دارد. جمله خطا را معمولا با حرف e یا d نمایش می‌دهند. به میزان خطای باقیمانده residual نیز گویند و در یک مدل مسیر با استفاده از جذر ۱-R² محاسبه می‌شود. منظور از R² ضریب تشخیص (ضریب تعیین) است که مجذور ضریب بتای استاندارد می‌باشد.

طراحی مدل مسیر

برای طراحی مسیر ابتدا متغیرهای مدل را مشخص کنید. سپس براساس فرضیه‌های تحقیق جهت روابط را تعیین کنید. بری آزمون فرضیه‌های تحقیق نیز از رگرسیون خطی ساده استفاده کنید. ضرایب بتا و مقادیر خطا را به مدل منتقل کنید. دقت کنید میزان همبستگی متغیرهای مستقل برونزا را با روش پیرسون تعیین کنید. بین متغیرهای مستقل برونزا یک فلش دو جهته وجود دارد که همان ضریب همبستگی پیرسون است.

یک مدل مسیر می‌تواند دارای متغیر میانجی (Mediator) باشد و حتی نقش متغیرهای تعدیلگر (Moderator) نیز می‌تواند بررسی شود.

خروجی این مرحله ممکن است مجموعه‌ای از فرضیه‌های مرتبط و یکپارچه باشد که معمولا از طریق ترسیمی و یا ریاضی بیان می‌شود.

در تحقیقات علوم اجتماعی مدلهای مفهومی معمولا به روش ترسیمی و نموداری بیان می‌شوند.

برای آزمون مدل مفهومی می‌توان از رگرسیون در نرم افزار spss استفاده نمود.

انواع روابط بین متغیرها در نمودار تحلیل مسیر

۱- اثر مستقیم: بیانگر یک اثر مستقیم متغیر x بر روی متغیر y است.

۲- اثر غیر مستقیم: یک اثر غیرمستقیم متغیر x بر روی y از طریق یک متغیر پیش‌بینی‌کننده دیگر.رابطه بین X و Y وقتى غیر مستقیم است که X علت Z است و Z نیز به نوبه خود در Y اثر دارد.

بسیاری از پژوهشگران مایلند اثر کلی یک متغیر را بر متغیر دیگر محاسبه کنند این کار از طریق جمع اثر مستقیم با مجموع آثار غیرمستقیم آن به دست می‌آید. آثار غیرمستقیم از طریق حاصلضرب ضرائب هر مسیر محاسبه می‌شود:

۳- اثر کاذب: رابطه بین X و Y وقتى کاذب (Spurious) است که Z علت هر دو متغیر X و Y باشد.

۴- اثرات تحلیل نشده: رابطه بین دو متغیر وقتى تحلیل نشده است که هر دوى آنها برونزا (exogenous) بوده و بنابراین تبیین تغییر پذیرى بین آنها توسط مدل امکان پذیر نباشد.

خلاصه و جمع‌بندی

برای اعتبارسنجی الگوی روابط علی میان یک مجموعه از متغیرها می‌توانید از تحلیل مسیر استفاده کنید. در این روش با استفاده از محاسبه ضریب بتای رگرسیون جهت و شدت روابط میان متغیرهای مدل قابل تبیین است. همچنین برای سنجش معناداری روابط می‌توانید از آماره تی استفاده کرده یا به مقدار معناداری مشاهده شده استناد کنید. برای انجام این روش باید پیش‌فرض‌هایی نیز لحاظ شود که در مقاله فوق اشاره گردید. در نهایت در مقایسه این روش با مدل معادلات ساختاری باید گفت مدل‌های ساختاری از اعتبار بیشتری برخوردار هستند.

برگرفته از پارس مدیر – نویسنده آرش حبیبی

دانلود کتاب آموزش تصویری تعیین حجم نمونه با Spss sample power نرم افزار