مدل معادلات ساختاری روشی برای بررسی روابط میان متغیرهای پنهان است که همزمان متغیرهای مشاهده‌پذیر را نیز در نظر می‌گیرد. منظور از متغیرهای پنهان همان عوامل اصلی هستند که در یک الگو یا مدل مفهومی نمایش داده می‌شوند. متغیرهای مشاهده‌پذیر نیز همان گویه‌ها یا سوالات مربوط به سنجش عوامل اصلی می‌باشند.

در واقع مدل معادلات ساختاری ترجمه فارسی Structural Equation Model است که به اختصار SEM نیز نامیده می‌شود. این روش یک ساختار علی ویژه بین مجموعه‌ای از متغیرهای پنهان و متغیرهای مشاهده‌پذیر است. با استفاده از روش مدل‌یابی معادلات ساختاری روابط بین متغیرهای پنهان با یکدیگر و نیز گویه‌های سنجش هر متغیر پنهان با متغیر مربوط قابل بررسی است. برای انجام محاسبات این روش از نرم‌افزار لیزرل یا نرم‌افزار اموس استفاده می‌شود.

روش مدل‌یابی معادلات ساختاری آن است که این روش برای ساخت مدل استفاده نمی‌شود بلکه برای ارزیابی و اعتبارسنجی مدل کاربرد دارد. در واقع پژوهشگر باید یک مدل اولیه را ترسیم کند سپس با استفاده از این روش به اعتبارسنجی مدل بپردازد. نظر به کاربرد وسیع این روش در مدیریت و علوم اجتماعی در این مقاله به تشریح کامل مدل معادلات ساختاری پرداخته شده است.

پیدایش مدل معادلات ساختاری

یکی از موضوعات اصلی پژوهش‌های مدیریت بررسی روابط بین عناصر بوده است. نخستین بار کارل پیرسون با ارائه روش همبستگی کوشش کرد تا روشی آماری برای بررسی روابط بین عناصر ارائه نماید. روش همبستگی پیرسون با وجود مزایایی که داشت اما روابط متغیرها را همواره دو به دو بررسی می‌کرد. در این روش نقش متغیرهای دیگر مدل در روابط میان سایر عناصر در نظر گرفته نمی‌شود. مدل‌های نظری چند متغیره را نمی‌توان با شیوه دو متغیری که هر بار تنها رابطه یک متغیر مستقل با یک متغیر وابسته در نظر گرفته می‌شود، ارزیابی کرد.

برای رفع این مشکل روش رگرسیون مطرح گردید. در روش‌های رگرسیونی بر خلاف روش‌های همبستگی نقش عناصر مختلف در رابطه عوامل موجود در مدل در نظر گرفته می‌شود. برای درک بهتر موضوع مقاله تفاوت رگرسیون و همبستگی را مطالعه کنید. اما نقطه ضعف اصلی روش رگرسیون و تحلیل مسیر نیز در عدم امکان در نظر گرفتن همزمان همه گویه‌های شکل دهنده متغیرهای اصلی بوده است. برای رفع این مشکل مدل معادلات ساختاری طراحی شد.

پیدایش مدل معادلات ساختاری

مدل معادلات ساختاری یکی از انواع تحلیل‌های همبستگی است که در دسته تحلیل ماتریس کوواریانس یا ماتریس همبستگی قرار می‌گیرد. تحلیل ماتریس کووایانس با توجه به هدف و نوع تحلیل به دو دسته اصلی تحلیل عاملی و مدل‌های ساختاری تقسیم می‌شود:

• تحلیل عاملی Factor Analysis
• مدل معادلات ساختاری Structural equation model, SEM

هر دو این تحلیل‌ها از طریق نرم افزار لیزرل و اموس قابل انجام است.

روش انجام مدل معادلات ساختاری

مدل معادلات ساختاری یا Structural Equation Model یک ساختار علی خاص بین مجموعه‌ای از سازه‌های غیرقابل مشاهده است. یک مدل معادلات ساختاری از دو مولفه تشکیل شده است: یک مدل ساختاری که ساختار علی بین متغیرهای پنهان را مشخص می‌کند و یک مدل اندازه‌گیری که روابطی بین متغیرهای پنهان و متغیرهای مشاهده شده را تعریف می‌کند.

گام‌های انجام تحقیق با تکنیک مدل‌یابی معادلات ساختاری عبارتند از:

• شناسایی متغیرهای اصلی تحقیق
• تهیه پرسشنامه برای سنجش متغیرها : تعیین گویه‌های سنجش هر متغیر اصلی
• تدوین فرضیه‌های تحقیق: تعیین روابط میان متغیرهای اصلی مدل
• طراحی مدل مفهومی براساس فرضیه‌های تحقیق
• توزیع پرسشنامه‌ها و گردآوری داده‌ها
•  طراحی مدل ساختاری و اجرای مدل با نرم افزار لیزرل یا اموس

متغیر پنهان و متغیر قابل مشاهده

سازه‌ها یا متغیرهای پنهان و آشکار دو مفهوم اساسی در تحلیل‌های آماری بویژه بحث تحلیل عاملی و مدل‌یابی معدلات ساختاری هستند.

متغیرهای پنهان Latent Variables که از آنها تحت عنوان متغیر مکنون نیز یاد می‌شود متغیرهائی هستند که به صورت مستقیم قابل مشاهده نیستند. برای مثال متغیر انگیزه را در نظر بگیرید. انگیزه فرد را نمی‌توان به صورت مستقیم مشاهده کرد و سنجید. به همین منظور برای سنجش متغیرهای پنهان از سنجه‌ها یا گویه‌هائی استفاده می‌کنند که همان سوالات پرسشنامه را تشکیل می‌دهند. این سنجه‌ها متغیرهای مشاهده شده هستند.

متغیرهای مشاهده پذیر Observed variables گویه‌ها یا سنجه‌هایی هستند که برای اندازه‌گیری متغیرهای پنهان استفاده می‌شوند. برای مثال سخت‌کوشی، حضور به‌موقع در محل کار، حساسیت به انجام کار و مواردی از این دست متغیرهای قابل مشاهده برای متغیر پنهان انگیزش هستند.

طراحی یک مدل معادلات ساختاری

طراحی یک مدل معادلات ساختاری با ذکر یک مثال توضیح داده می‌شود. برای نمونه در پژوهشی رابطه سه متغیر پنهان A,B,C بررسی می‌شود. رابطه علی بین این متغیرها به این صورت در نظر گرفته شده است:
۱- متغیر پنهان A یک متغیر مستقل است و بر هر دو متغیر پنهان B و C تاثیر دارد.
۲- برای سنجش متغیر پنهان A از دو متغیر قابل مشاهده A1 و A2 استفاده شده است.
۳- برای سنجش متغیر پنهان B از دو متغیر قابل مشاهده B1 و B2 استفاده شده است.
۴- برای سنجش متغیر پنهان C از سه متغیر قابل مشاهده C1 و C2 و C3 استفاده شده است.

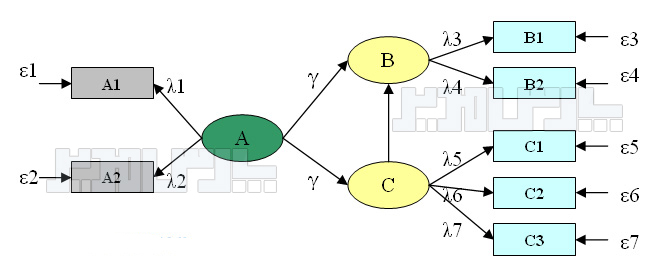
ساختار کلی مدل معادلات ساختاری؛ منبع: حبیبی، ۱۳۹۵ ص ۱۰

مدل کلی معدلات ساختاری از الگوی شکل ۲-۳ پیروی می‌کند. قوانین این الگو عبارتند از:

۱- هر بیضی در مدل معادلات ساختاری نشان‌دهنده یک متغیر پنهان است.

۲- هر مستطیل در مدل معادلات ساختاری نشان‌دهنده یک متغیر قابل مشاهده است.

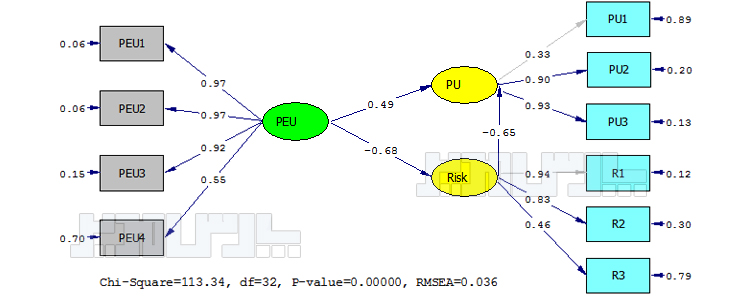
۳- از هر متغیر پنهان(بیضی) به هر متغیرقابل مشاهده(مستطیل) پیکانی وجود دارد که با نماد λ نشان داده می‌شود. به λ وزن‌های عاملی یا بار عاملی گفته می‌شود. طبق گفته کلاین بارهای عاملی بزرگتر از ۰.۳ نشان‌دهنده با اهمیت بودن رابطه است.

۴- هر مقدار ε نیز نشان‌دهنده خطا در پیش‌بینی متغیرهای پنهان از یکدیگر است.

۵- ضریب رابطه علی بین دو متغیر پنهان مستقل و وابسته با γ نشان داده می‌شود.

۶- ضریب رابطه علی بین دو متغیر پنهان وابسته با β نشان داده می‌شود.

بار عاملی (Factor Loading)

قدرت رابطه بین عامل (متغیر پنهان) و متغیر قابل مشاهده بوسیله بار عاملی نشان داده می‌شود. بار عاملی مقداری بین صفر و یک است. اگر بار عاملی کمتر از ۰.۳ باشد رابطه ضعیف درنظر گرفته شده و از آن صرف‌نظر می‌شود. بارعاملی بین ۰.۳ تا ۰.۶ قابل قبول است و اگر بزرگتر از ۰.۶ باشد خیلی مطلوب است. (کلاین، ۱۹۹۴)
بار عاملی در شکل با λ نشان داده شده است. در تحلیل عاملی متغیرهائی که یک متغیر پنهان (عامل) را می‌سنجند، باید با آن عامل، بار عاملی بالا و با سایر عامل‌ها، بار عاملی پائین داشته باشند. در نرم‌افزار لیزرل بار عاملی از طریق گزینه Standardized solution از لیست Stimates محاسبه می‌شود.

جهت بررسی معنادار بودن رابطه بین متغیرها از آماره آزمون t یا همان t-value استفاده می‌شود. چون معناداری در سطح خطای ۰.۰۵ بررسی می‌شود بنابراین اگر میزان بارهای عاملی مشاهده شده با آزمون t-value از ۱.۹۶ کوچکتر محاسبه شود، رابطه معنادار نیست و در نرم افزار لیزرل با رنگ قرمز نمایش داده خواهد شد.

ویدیوی آموزش مدل ساختاری

خلاصه و جمع‌بندی

مدل‌یابی معادلات ساختاری یک روش آماری برای اعتبارسنجی مدل مفهومی پژوهش است. پژوهشگر ابتدا باید عوامل مختلف شکل‌دهنده پدیده مورد بررسی را شناسایی کند. سپس براساس مبانی نظری موجود روابط بین عوامل را حدس بزند و فرضیه‌سازی کند. همچنین برای هر عامل باید تعدادی گویه جهت سنجش شناسایی کند. پس از فرضیه‌سازی و ترسیم مدل مفهومی اولیه، این مدل باید در محیط نرم‌افزار اموس یا لیزرل پیاده‌سازی شود. در نهایت با استفاده از روش مدل معادلات ساختاری می‌توان مدل مفهومی را اعتبارسنجی کرد.

منبع: کتاب مدل یابی معادلات ساختاری نوشته آرش حبیبی انتشارات جهاد دانشگاهی