مفهوم تحلیل خوشه ای چیست؟
طبقه بندی پدیدهها یا متغیرها از ارکان هر علمی است و تحلیل خوشهای یکی از روشهای تحلیل چند متغیره است که برای طبقه بندی عناصر یا متغیرها و تشخیص گروههای همگن به کار میرود. تحلیل خوشهای طبقه بندی عناصر یا متغیرها به گروههای همگن است به گونهای که عناصر (یا متغیرهای) هر گروه دارای بیشترین شباهت با هم و کمترین شباهت با عناصر (یا متغیرهای) گروههای دیگر باشند.
تحلیل خوشهای روشهای مختلفی دارد که یکی از پرکاربردترین آنها روش خوشه بندی سلسله مراتبی است. طبقه بندی متغیرها را نیز به خوبی میتوان با تحلیل عامل انجام داد. از این رو در اینجا فقط به معرفی تحلیل خوشهای سلسله مراتبی عناصر میپردازیم.در ادامه تحلیل خوشهای سلسله مراتبی عناصر را به اختصار تحلیل خوشهای میخوانیم.
تحلیل خوشهای اساساً برای طبقه بندی عناصر بر حسب متغیر یا متغیرهای کمّی است چه متغیرهای کیفی فیالنفسه دارای طبقه بندی هستند مانند جنسیت با دو طبقه زن و مرد یا نگرشهای اجتماعی با دو طبقه موافق و مخالف یا سه طبقه موافق و بینظر و مخالف یا پنج طبقه کاملاً موافق و موافق و بینظر و مخالف و کاملاً مخالف.
اما وقتی با متغیر کمّی سروکار داریم مجموعهای (دامنهای) از مقادیر داریم که برای طبقه بندی آن یا در واقع طبقه بندی عناصر بر حسب آن ناگزیریم از روشی برای طبقه بندی استفاده کنیم. به طور کلی متغیر کمّی پیوسته را میتوان هم به طور ساده طبقه بندی کرد و هم با تحلیل خوشهای.
متغیر کمّی پیوسته را میتوان به طور ساده به سه صورت طبقه بندی کرد: طبقه بندی همعرض و طبقه بندی همفراوانی و طبقه بندی متوازن. در اینجا با یک مثال ساده (مثال۱) این طبقه بندیها را به اختصار توضیح میدهیم و با طبقه بندی تحلیل خوشهای مقایسه میکنیم.
تعریف ۱: تحلیل خوشهای سلسله مراتبی عناصر طبقه بندی عناصر برحسب همگنی در یک یا چند متغیر کمّی است.
در طبقه بندی همعرض عرض همه طبقات را یکسان میگیریم. به این منظور ابتدا مقادیر عناصر (دادهها) را به ترتیب نزولی مرتب میکنیم و دامنه مقادیر (تفاضل مقدار حداکثر از حداقل به اضافه یک) را پیدا کرده و سپس آن را بر تعداد مورد نظر تقسیم میکنیم تا عرض طبقات با نماد W به دست آید:
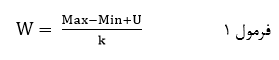
که در آن Max مقدار حداکثر است وMin مقدار حداقل توزیع متغیر کمّی وU واحد گرد شدن مقادیر وK تعداد طبقات که بنابر مقتضیات تحقیق تعیین میشود.
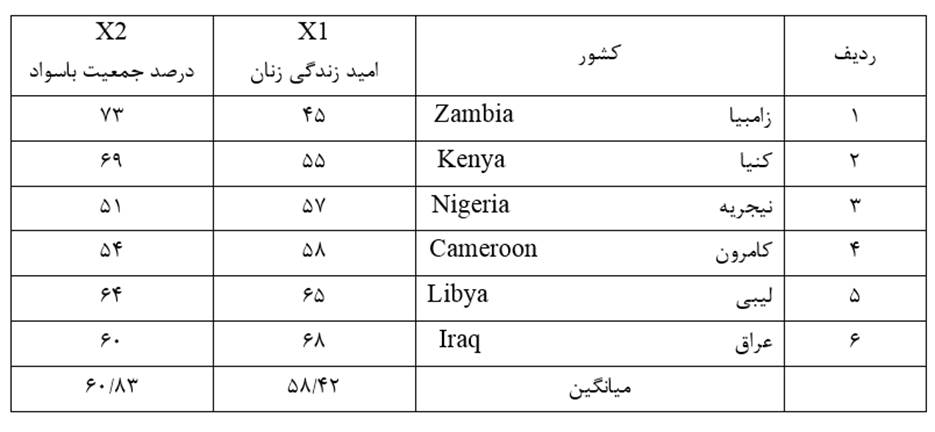
مثال 1: دادههای جدول 1 توزیع امید به زندگی زنان (X1) و درصد جمعیت باسواد (X2) نمونهای از کشورهای جهان در سال 1995 است. عرض طبقات در طبقه بندی همعرض متغیر X1 (امید زندگی زنان) مثال 1 چنانچه تعداد طبقات را 3 در نظر بگیریم عبارت است از:
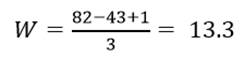
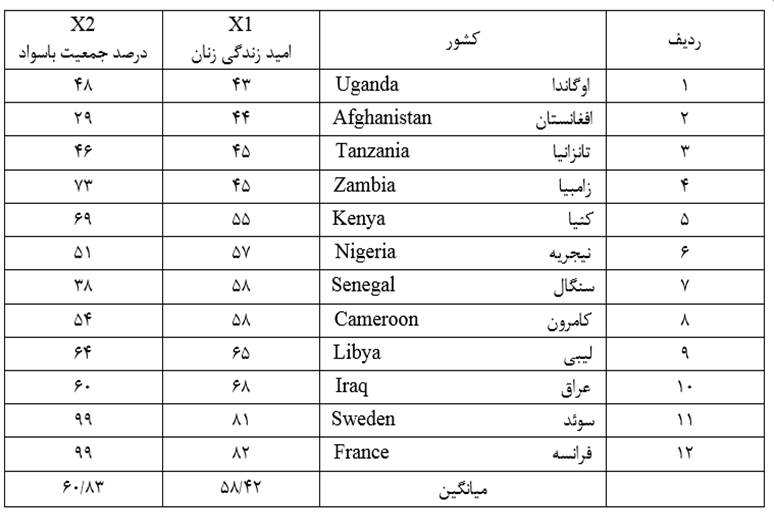
عرض طبقات در طبقه بندی همعرض امید زندگی زنان 13/3 است که اگر به واحد گرد شدن مقادیر متغیر که در اینجا یکان است گرد کنیم 13 میشود. با طبقه بندی متغیر X1 (امید زندگی زنان) به سه طبقه هم عرض جدول 2 میرسیم.

طبقه بندی هم فراوانی و کاربرد آن در تحلیل خوشه ای
در طبقه بندی همفراوانی، فراوانی همه طبقات را یکسان میگیریم. به این منظور کل فراوانی را به تعداد طبقات مورد نظر تقسیم میکنیم تا به طبقاتی برسیم که فراوانی آنها یکسان (F) است:

که در آن N کل فراوانی است و K تعداد طبقات که بنابر مقتضیات تحقیق تعیین میشود.
به عنوان مثال فراوانی یکسان طبقات در طبقه بندی همفراوانی متغیر X1 (امید زندگی زنان) جدول 1 چنانچه تعداد طبقات را 3 در نظر بگیریم عبارت است از:
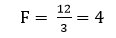
سپس براساس دادههایی که به ترتیب نزولی مرتب شده است حدود هر طبقه را براساس مقدار حداقل و حداکثر موردهای آن طبقه تشکیل میدهیم مانند جدول۳.
طبقه بندی متوازن موازنهای بین دو نوع طبقه بندی پیشین است. در طبقه بندی متوازن سعی میشود موازنهای بین عرض طبقات و فراوانی آنها برقرار گردد. طبقه بندی طوری صورت میگیرد که حتیالامکان نه عرض طبقات ناهمگون شود و نه فراوانی آنها.
خوشه بندی چیست و چه کاربردی دارد؟
اما خوشه بندی نوعی طبقه بندی پیشرفته است که براساس میزان تشابه و همگنی عنصرها در یک یا چند متغیر صورت میگیرد.
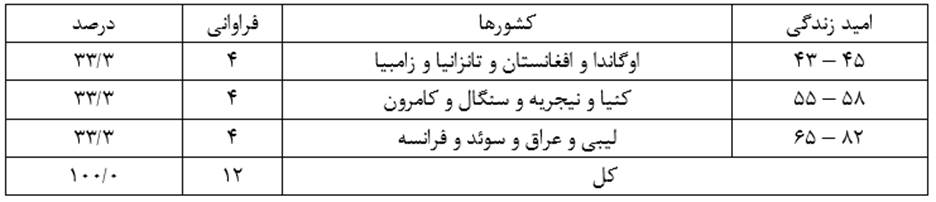
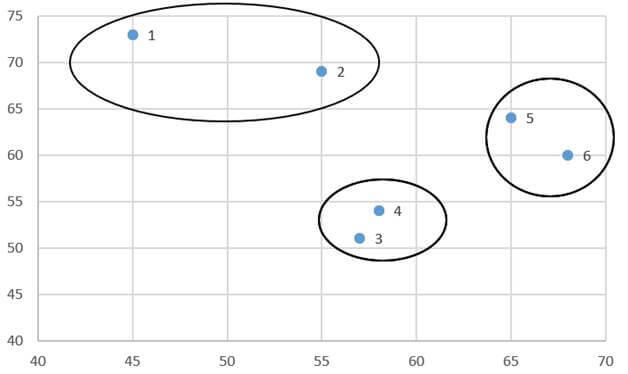
به عنوان مثال با خوشه بندی عناصر (کشورهای) مثال 1 برحسب متغیر X1 (امید زندگی زنان) به سه طبقه به طبقات همگن جدول 4 میرسیم: طبقه اول شامل چهار کشور اوگاندا و افغانستان و تانزانیا و زامبیاست که امید زندگی زنان آنها بین 43 الی 45 سال است. طبقه دوم شامل شش کشور کنیا و نیجریه و سنگان و کامرون و لیبی و عراق است که امید زندگی زنان آنها بین 55 تا 68 سال است. طبقه سوم شامل دو کشور سوئد و فرانسه است که امید زندگی زنان آنها بین 81 الی 82 سال است.

تکنیک خوشه بندی نه تنها متغیر کمّی را بر حسب همگنی عناصر به تعداد طبقات مورد نظر محقق تقسیم میکند بلکه متغیر را در سطوح مختلف همگنی عناصر به صورت یک نمودار درختی طبقه بندی میکند. این امر به محقق کمک میکند تا با مقایسه طبقه بندی سطوح مختلف مناسبترین طبقه بندی را انتخاب کند.
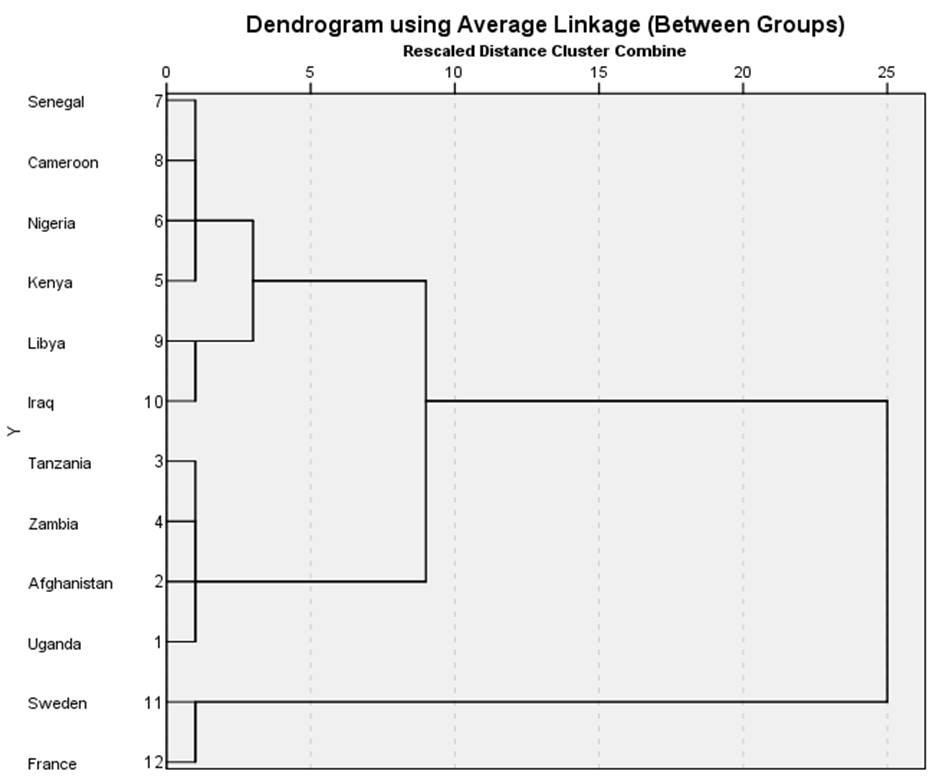
به عنوان مثال با خوشه بندی عناصر (کشورهای) مثال 1 برحسب متغیر X1 (امید زندگی زنان) نمودار درختی شکل 1 ارائه میشود. همانطور که در این شکل میبینیم در سطح اول هریک از کشورها (عناصر) یک طبقه مجزا را تشکیل میدهد.
در سطح دوم کشورها به چهار طبقه تقسیم شدهاند: طبقه اول شامل چهار کشور سنگال و کامرون و نیجریه و کنیا و طبقه دوم شامل دو کشور عراق و لیبی و طبقه سوم شامل چهار کشور تانزانیا و زامبیا و افغانستان و اوگاندا و طبقه چهارم شامل دو کشور سوئد و فرانسه.
در سطح سوم کشورها به سه طبقه تقسیم شدهاند: طبقه اول شامل شش کشور سنگال و کامرون و نیجریه و کنیا و عراق و لیبی و طبقه دوم شامل چهار کشور تانزانیا و زامبیا و افغانستان و اوگاندا و طبقه سوم شامل دو کشور سوئد و فرانسه.
در سطح چهارم کشورها به دو طبقه تقسیم شدهاند: طبقه اول شامل ده کشور سنگال و کامرون و نیجریه و کنیا و عراق و لیبی و تانزانیا و زامبیا و افغانستان و اوگاندا و طبقه دوم شامل دو کشور سوئد و فرانسه.
به این ترتیب در این مثال میبینیم براساس میزان تشابه کشورها (عناصر) در متغیر امید زندگی زنان سه نوع طبقه بندی ارائه شده است (چهار طبقهای و سه طبقهای و دو طبقهای) و ما میتوانیم با مقایسه آنها و وجه نظری و مفهومی آنها طبقه بندی مناسب را انتخاب کنیم.
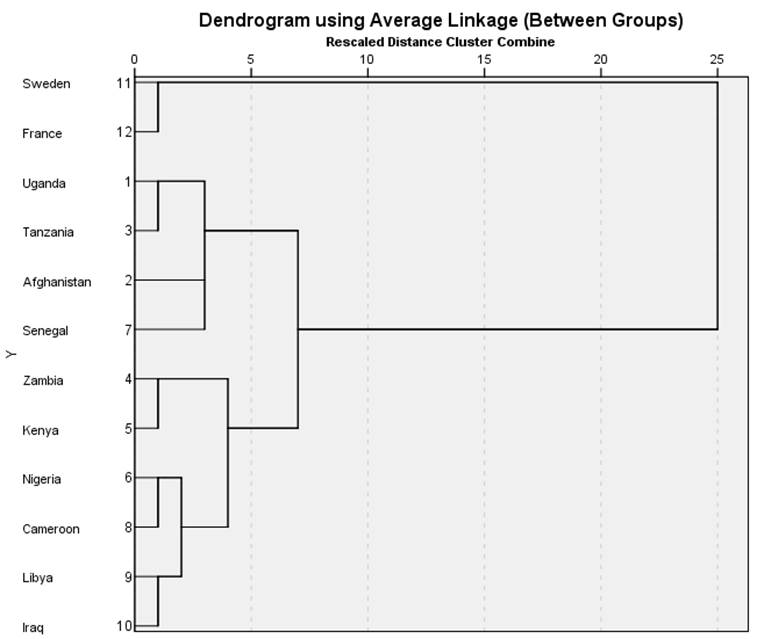
اما مزیت اصلی و عمده تکنیک خوشه بندی این است که با این تکنیک میتوان عناصر را برحسب ترکیبی از چند متغیر نیز طبقه بندی کرد. به عنوان مثال با خوشه بندی عناصر (کشورهای) مثال 1 بر حسب دو متغیر X1 (امید زندگی زنان) و X2 (درصد جمعیت باسواد) نمودار درختی شکل 2 ارائه میشود. همانطور که در این شکل میبینیم طبقه بندی عناصر مثال 1 برحسب دو متغیر X1 و X2 با طبقه بندی آنها صرفاً برحسب متغیر X1 نسبتا متفاوت است.
مراحل تحلیل خوشهای
تحلیل خوشهای شامل دو مرحله اصلی است: تعیین اندازه شباهت جفت جفت عناصر مورد تحلیل و سرانجام خوشه بندی عناصر براساس اندازه شباهت با استفاده از یکی از روشهای خوشه بندی.
تعیین اندازه شباهت و ضرایب آن ها
در تحلیل خوشهای طبقه بندی براساس اندازه شباهت عناصر صورت میگیرد. اندازه شباهت مقدار نزدیکی یا دوری عناصر نسبت به یکدیگر است که با دو دسته از ضرایب سنجیده میشود: یکی ضرایب عدم تشابه و دیگری ضرایب تشابه. ضرایب عدم تشابه مبتنی بر اندازه فاصله و دوری هر عنصر از عنصر دیگر است. معمولا برای تحلیل خوشهای از این نوع ضرایب استفاده میشود. ضرایب تشابه هم مبتنی بر نزدیکی هر عنصر از عنصر دیگر است.
ضرایب عدم تشابه
ضرایب عدم تشابه انواع گوناگونی دارد که مهم ترین آنها عبارتند از مجذور فاصله اقلیدسی و فاصله اقلیدسی و فاصله بلوک شهر و فاصله چبایچوف.
مجذور فاصله اقلیدسی
مجذور فاصله اقلیدسی (با نماد eij۲) دوعنصر در مجموعهای از متغیرها عبارت است از مجموع مجذور تفاوت مقادیر دو عنصر در هریک از متغیرها:

که در آن Xi مقدارعنصر i ام و Xj عنصر i ام در متغیر X است.
به عنوان مثال مجذور فاصله اقلیدسی دو عنصر اول و دوم (کشور اوگاندا و افغانستان) مثال 1 در دو متغیر امید زندگی (X1) و درصد جمعیت باسواد (X2) عبارت است از:
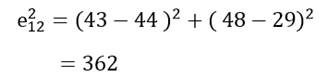
یا مجذور فاصله اقلیدسی دو عنصر چهارم و پنجم (کشور زامبیا و کنیا) عبارت است از:
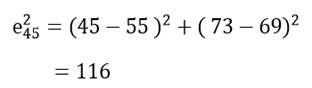
دامنه مجذور فاصله اقلیدسی از صفر (شباهت کامل) تا بینهایت (عدم تشابه کامل) است.
فاصله اقلیدسی
فاصله اقلیدسی (با نماد eij) دوعنصر در مجموعهای از متغیرها عبارت است از جذر مجموع مجذور تفاوت مقادیر دو عنصر در هریک از متغیرها:
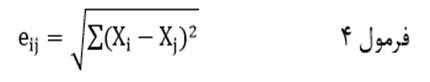
که در آن Xi مقدار عنصر i ام و Xj مقدار عنصر j ام در متغیرX است.
به عنوان مثال فاصله اقلیدسی دو عنصر اول و دوم (کشور اوگاندا و افغانستان) مثال 1 در دو متغیر امید زندگی (X1) و درصد جمعیت باسواد (X2) عبارت است از:
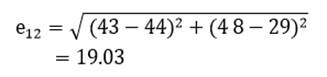
دامنه فاصله اقلیدسی هم از صفر (شباهت کامل) تا بینهایت (عدم تشابه کامل) است.
فاصله بلوک
فاصله بلوک شهر یا اختصاراً فاصله بلوک (با نماد blij) دو عنصر در مجموعهای از متغیرها عبارت است از مجموع قدر مطلق تفاوت مقادیر دو عنصر در هریک از متغیرها:

که در آن Xi مقدار عنصر i ام و Xj مقدار عنصر jام در متغیر X است.
به عنوان مثال فاصله بلوک دو عنصر اول و دوم (کشور اوگاندا و افغانستان) مثال 1 در دو متغیر امید زندگی (X1) و درصد جمعیت باسواد (X2) عبارت است از:
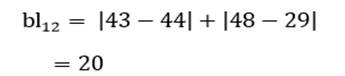
دامنه فاصله بلوک هم از صفر (شباهت کامل) تا بینهایت (عدم تشابه کامل) است.
فاصله چبایچوف
فاصله چبایچوف (با نماد chij) دوعنصر در مجموعهای از متغیرها عبارت است از بزرگ ترین قدر مطلق تفاوت مقادیر دو عنصر در بین متغیرها:
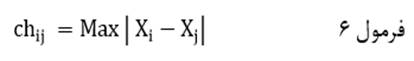
که در آن Xi مقدار عنصر i ام و Xj مقدار عنصر j ام در متغیر X است و max بزرگترین (حداکثر) تفاوت مقادیر دو عنصر در بین متغیرها.
به عنوان مثال فاصله چبایچوف دو عنصر اول و دوم (کشور اوگاندا و افغانستان) مثال 1 در دو متغیر امید زندگی (X1) و درصد جمعیت باسواد (X2) عبارت است از:
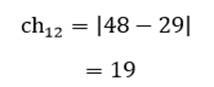
دامنه فاصله چبایخوف هم از صفر (شباهت کامل) تا بینهایت (عدم تشابه کامل) است.
ضرایب تشابه
ضرایب عدم تشابه انواع گوناگونی دارد که در اینجا یکی از مهم ترین آنها را که کسینوس بردار مقادیر است معرفی میکنیم.
کسینوس بردار مقادیر
کسینوس بردار مقادیر (با نماد coij) دو عنصر در مجموعهای از متغیرها عبارت است از مجموع حاصلضرب مقادیر دو عنصر در هریک از متغیرها تقسیم بر جذر مجموع مجذور مقدار یک عنصر در متغیرها ضرب در مجموع مجذور مقدار عنصر دیگر در متغیرها:
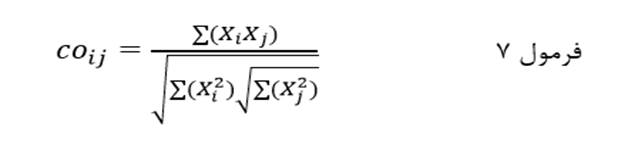
که در آن Xi مقدار i ام و Xj مقدار عنصرj ام در متغیر X است.
به عنوان مثال کسینوس بردار مقادیر دو عنصر اول و دوم (کشور اوگاندا و افغانستان) مثال 1 در دو متغیر امید زندگی (X1) و درصد جمعیت باسواد (X2) عبارت است از:
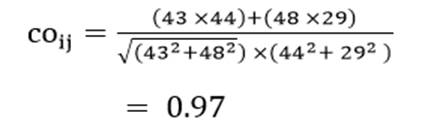
دامنه مقادیر کسینوس بردار از ۱- (عدم تشابه کامل) تا ۱+ (تشابه کامل) است.
خوشه بندی عناصر آخرین مرحله تحلیل خوشه ای
خوشه بندی عناصر مرحله اصلی و نهایی تحلیل خوشهای است. در این مرحله عناصر بر اساس شباهتشان به هم طبقه بندی میشوند. در خوشه بندی ابتدا همه عناصر خوشههای گوناگونی به حساب میآیند.
سپس دو خوشهای که دارای کمترین فاصله (بیشترین شباهت) به هم هستند با هم ادغام میشوند و یک خوشه جدید تشکیل میدهند. باز در مرحله بعدی دو خوشه که دارای کمترین فاصله هستند با هم ادغام میشوند و خوشه جدید دیگری تشکیل میدهند. این ادغام دو خوشه در هر مرحله و تشکیل خوشههای بزرگتر متوالیاً ادامه مییابد و سرانجام به ترکیب تمام خوشهها و رسیدن به یک خوشه میرسد.
خوشهبندی نیز با روشهای گوناگونی صورت میگیرد. در هر روش نیز برای اندازه شباهت عناصر میتوان هر یک از ضرایب تشابه یا ضرایب عدم تشابه را به کار برد. با وجود این معمولاً ضریب مجذور فاصله اقلیدسی برای اندازه شباهت خوشهها استفاده میشود.
مقایسه روش های خوشه بندی
رایجترین روشهای خوشهبندی عبارتند از متوسط گروهی و متوسط درونگروهی و تک اتصالی و تام اتصالی و وارد. در بین این روشها روش خوشهبندی تک اتصالی خوشهبندی منقبض (نزدیک به هم) تولید میکند و روش خوشهبندی تام اتصالی خوشهبندی منبسط (دور از هم). اما روش خوشهبندی متوسط گروهی خوشهبندی متعادلی بین این دو تولید میکند. از این رو محققان بیشتر روش متوسط گروهی را به کار میبرند. روش خوشهبندی وارد نیز بعد از روش متوسط گروهی پرکاربردترین روش خوشهبندی است.
روش متوسط گروهی
در روش متوسط گروهی که عنوان اختصاری روش جفت گروهی ناموزون با استفاده از متوسط حسابی(UPGMA) است و اتصال بین گروهی هم خوانده میشود در هر مرحله خوشهبندی فاصله بین جفت جفت خوشهها بر اساس ضریب متوسط گروهی احتساب میشود. سپس دو خوشهای که دارای کمترین فاصله هستند با هم ترکیب میشوند.
ضریب متوسط گروهی با نماد ga(i)(j) هم عبارت است از مجموع اندازه شباهت عناصر یک خوشه با عناصر خوشه دیگر تقسیم بر تعداد اندازه شباهت عناصر دو خوشه:
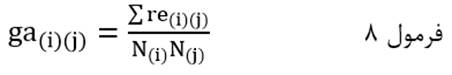
که در آن re(i)(j) اندازه شباهت عنصری از خوشه (i) ام با عنصری از خوشه (j) ام است و N(i)N(j) که حاصلضرب تعداد عناصر خوشه (i) ام در تعداد عناصر خوشه (j) ام است تعداد اندازه شباهت عناصر دو خوشه است.
در ادامه عناصر مثال ۲ را که برای سادگی محاسبات بخشی از کشورهای مثال ۱ است با روش متوسط گروهی خوشهبندی میکنیم و اندازه شباهت عناصر را هم مجذور فاصله اقلیدسی عناصر میگیریم.
مثال ۲: دادههای جدول 5 توزیع امید زندگی زنان (X1) و درصد جمعیت باسواد (X2) نمونهای از کشورهای جهان در سال 1995 است. جدول 6 هم ماتریس اندازه شباهت عناصر (کشورها) بر حسب دو متغیر مذکور است که مبتنی بر مجذور فاصله اقلیدسی است.
مرحله صفر در خوشه بندی
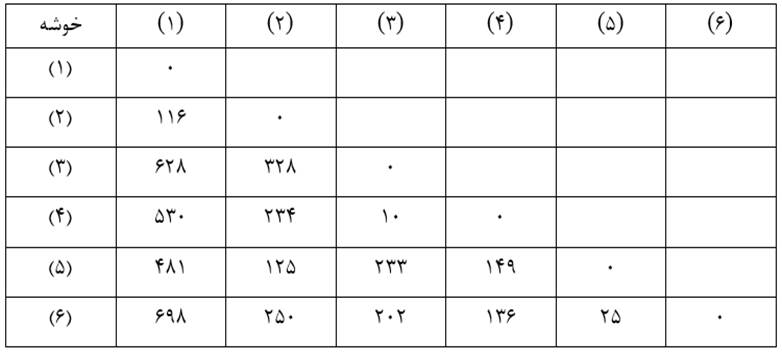
در ابتدای خوشهبندی که مرحله صفر خوانده میشود هر عنصر یک خوشه به حساب میآید. در این مرحله ضریب متوسط گروهی دو خوشه همان اندازه شباهت دو عنصر است. به عنوان مثال ضریب متوسط گروهی خوشه (۱) با خوشه (۲) بر مبنای مجذور فاصله اقلیدسی عناصر دو خوشه (جدول ۶) عبارت است از:
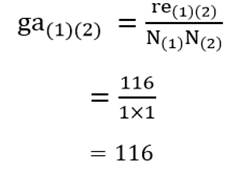
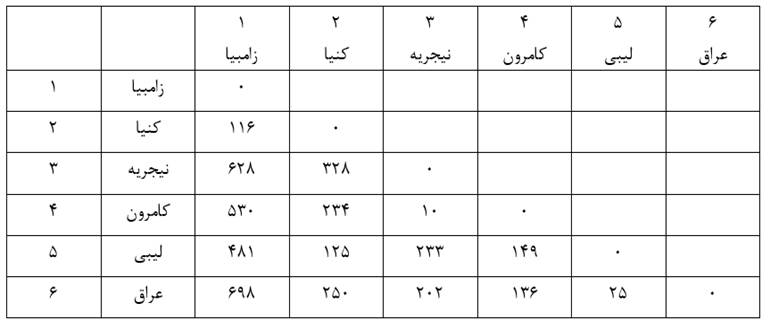
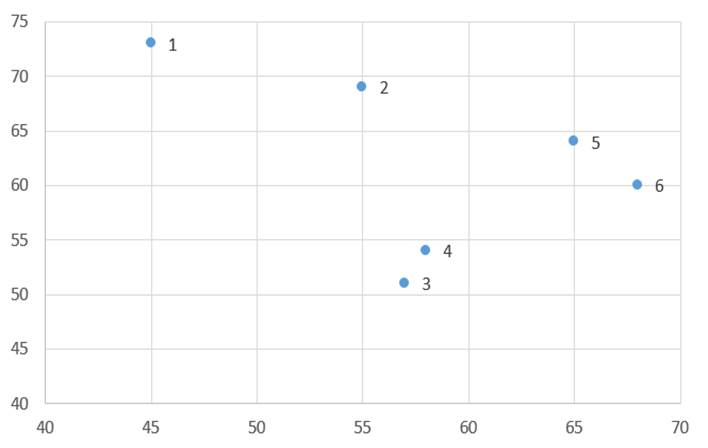
خوشهبندی مرحله صفرمثال ۲ را میتوان به صورت نمودار فاصله خوشهها نشان داد (شکل۳). جدول ۷ هم ماتریس فاصله خوشهها بر حسب ضریب متوسط گروهی در مرحله صفر است که مانند ماتریس اندازه شباهت عناصر (جدول۷) است.
مرحله یک
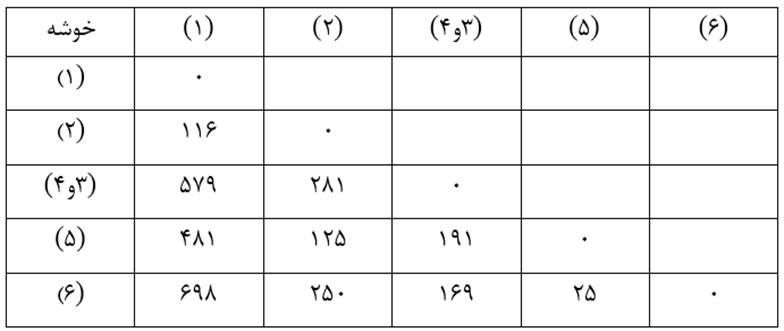
در مرحله یک با وارسی فاصله خوشههای مرحله صفر (جدول ۷) میبینیم دو خوشه (۳) و (۴) دارای کمترین فاصله هستند. ضریب متوسط گروهی آنها ۱۰ است که کمترین ضریب متوسط گروهی است. از این رو این دو خوشه را با هم ترکیب میکنیم (شکل ۴).
در این مرحله ضریب متوسط گروهی خوشههای مرحله قبل همان اندازههای قبلی است و فقط باید ضریب متوسط گروهی خوشه جدید (۳و۴) را با بقیه خوشهها احتساب کنیم.
ضریب متوسط گروهی خوشه (۱) با خوشه (۳و۴) با توجه به ماتریس اندازه شباهت عناصر (جدول ۶) عبارت است از:
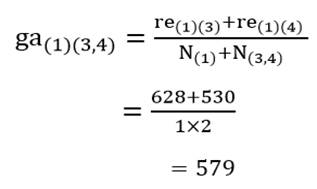
و خوشه (۲) با خوشه (۳و۴):
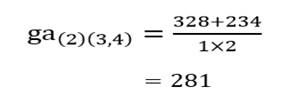
و خوشه (۵) با خوشه (۳و۴):
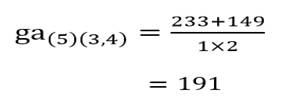
و خوشه (۶) با خوشه (۳و۴):
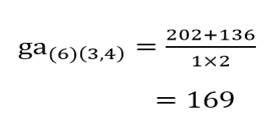
حال ماتریس فاصله خوشههای مرحله یک را تشکیل میدهیم (جدول ۸)
مرحله دو
در این مرحله با وارسی ماتریس فاصله خوشههای مرحله قبل (جدول ۸) میبینیم دو خوشه (۵) و خوشه (۶) دارای کمترین ضریب متوسط گروهی هستند. از این رو این دو خوشه را با هم ترکیب میکنیم (شکل ۵).
در مرحله ۲ هم ضریب متوسط گروهی خوشههای گروهی خوشههای مرحله قبل همان اندازههای قبلی است و فقط باید ضریب متوسط گروهی خوشه جدید (۵ و۶) را با بقیه خوشهها احتساب کنیم.
ضریب متوسط گروهی خوشه (۱) با خوشه (۵ و۶) با توجه به ماتریس اندازه شباهت عناصر(جدول ۶) عبارت است از:
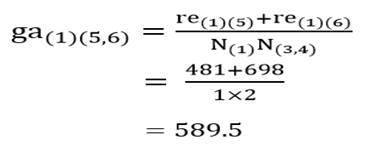
و ضریب متوسط گروهی خوشه (۲) با خوشه (۵ و۶):
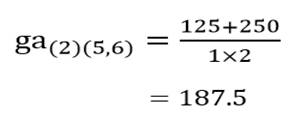
و ضریب متوسط گروهی خوشه (۳ و۴) با خوشه (۵ و۶):
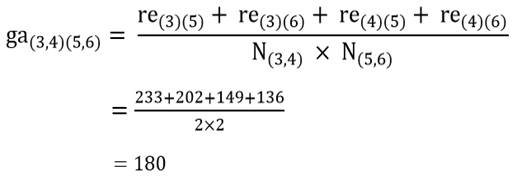
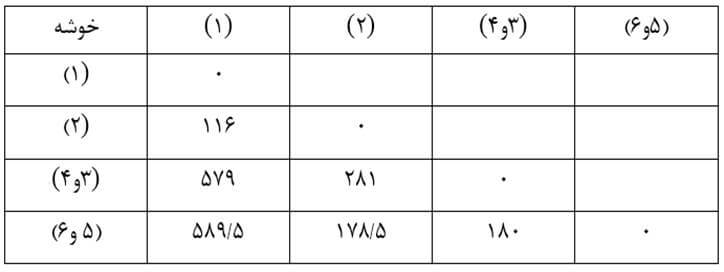
حال ماتریس فاصله خوشههای مرحله ۲ را تشکیل میدهیم (جدول ۹).
مرحله سه
در مرحله ۳ با وارسی ماتریس فاصله خوشههای مرحله قبل (جدول ۹) میبینیم دو خوشه (۱) و (۲) دارای کمترین فاصله خوشهها (۱۱۶) هستند. از این رو این دو خوشه را با هم ترکیب میکنیم (شکل ۶).
در این مرحله هم ضریب متوسط گروهی خوشه جدید (۱و۲) را با بقیه خوشهها احتساب کنیم. ضریب متوسط گروهی خوشه (۱و۲) با خوشه (۳و۴) با توجه به ماتریس اندازه شباهت عناصر (جدول ۶) عبارت است از:
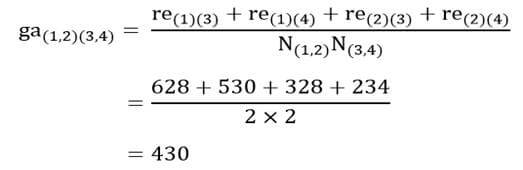
و خوشه (۱و۲) با خوشه (۵ و۶):
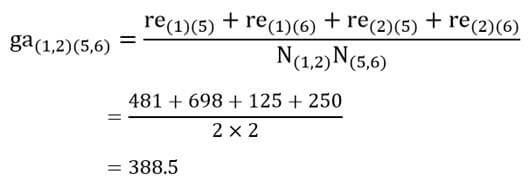
حال ماتریس فاصله خوشههای مرحله سه را تشکیل میدهیم (جدول ۱۰).

مرحله چهار
در این مرحله هم با وارسی ماتریس فاصله خوشههای مرحله قبل (جدول ۱۰) میبینیم دو خوشه (۳و۴) و (۵و۶) دارای کمترین ضریب متوسط گروهی (۱۸۰) هستند. از این رو این دو خوشه را با هم ترکیب میکنیم (شکل ۷).
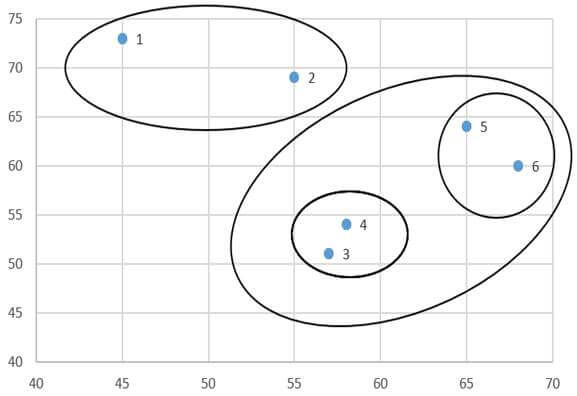
در مرحله چهار فقط باید ضریب متوسط گروهی خوشه جدید (۳و۴و۵و۶) را با خوشه (۱و۲) را احتساب کنیم. ضریب متوسط گروهی خوشه (۱و۲) با خوشه (۳و۴و۵و۶) با توجه به ماتریس اندازه شباهت عناصر (جدول ۶) عبارت است از:
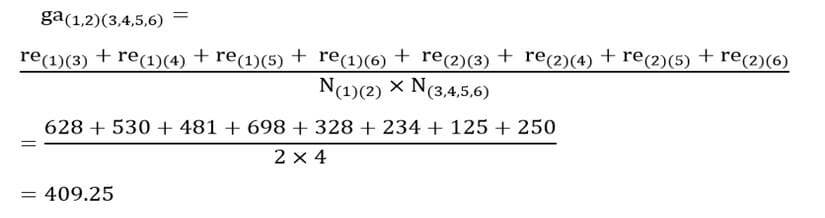
حال ماتریس فاصله خوشههای مرحله چهار را تشکیل میدهیم (جدول ۱۱).
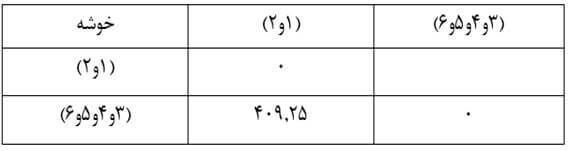
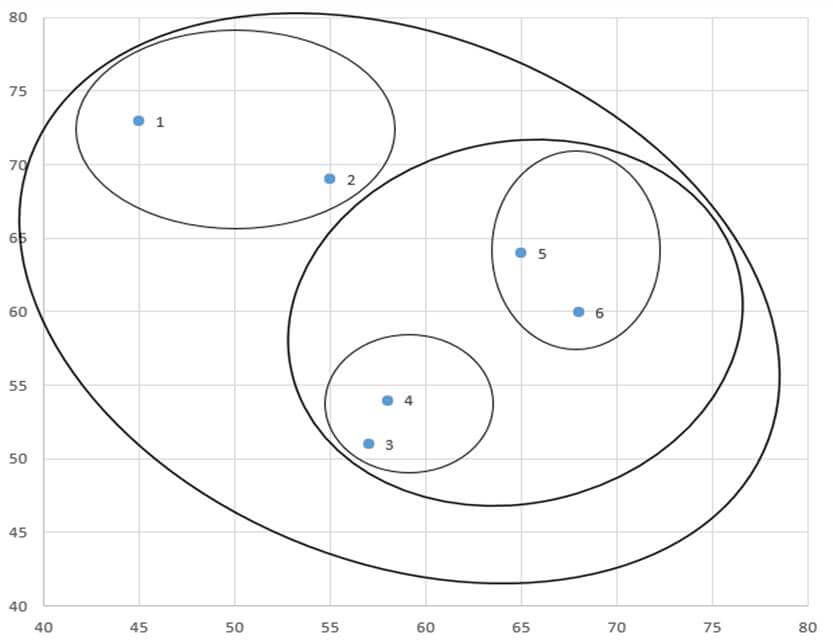
مرحله پنج
در این مرحله با ترکیب دو خوشه (۳و۴و۵و۶) و(۱و۲) که فاصله آن دو بر حسب ضریب متوسط گروهی ۴۰۹/۲۵ است به خوشه نهایی میرسیم که تمام عناصر را در بر میگیرد (شکل ۸).
نمودار درختی متوسط گروهی
تمام مراحل خوشهبندی را میتوان به طور مختصر در نمودار درختی نشان داد مانند شکل ۹ که نمودار درختی خوشهبندی با روش متوسط گروهی مثال ۲ است. در این نمودار درختی میبینیم در ابتدا هر عنصری یک خوشه است. در مرحله ۱ خوشه (۳) و خوشه (۴) در فاصله (ضریب متوسط گروهی) ۱۰ با هم ترکیب شدهاند. سپس در مرحله ۲ خوشه (۵) و خوشه (۶) در فاصله ۲۵ با هم ترکیب شدهاند.
در مرحله ۳ خوشه (۱) و خوشه (۲) در فاصله ۱۱۶ با هم ترکیب شدهاند. در مرحله ۴ خوشه (۳و۴) و خوشه (۵و۶) در فاصله ۱۸۰ با هم ترکیب شدهاند. سرانجام در مرحله ۵ خوشه (۳و۴و۵و۶) و خوشه (۱و۲) در فاصله ۴۰۹ با هم ترکیب شدهاند.
این ارائه یکپارچه خوشهبندی روابط بین خوشهها را به سهولت به ما نشان میدهد. به عنوان مثال نمودار درختی مثال ۲ (شکل۹) نشان میدهد که عناصر خوشه (۳و۴) به هم نزدیکترند تا عناصر خوشه (۵و۶). به بیان دیگر خوشه (۳و۴) همگنتر از خوشه (۵و۶) است. همینطور دو خوشه (۳و۴) و (۵و۶) همگنتر از خوشه (۱و۲) هستند. گذشته از این دو خوشه (۳و۴) و(۵و۶) به هم نزدیکترند تا به خوشه (۱و۲).
به این ترتیب نمودار درختی خوشهبندی به محقق کمک میکند تا با توجه به روابط خوشهها و فاصله خوشهها از بین سطوح مختلف طبقهبندی (خوشهبندی) آن سطحی را که مناسبتر میبیند انتخاب کند.
روش متوسط درونگروهی
روش متوسط درون گروهی که اتصال درونگروهی نیز خوانده میشود مانند روش متوسط گروهی است با این تفاوت که اندازه شباهت عناصر درون خوشهها نیز به حساب میآید. در این روش فاصله بین خوشهها با ضریب متوسط درونگروهی احتساب میشود. سپس دو خوشهای که دارای کمترین فاصله هستند با هم ترکیب میشوند.
ضریب متوسط درونگروهی با نماد wga(i)(j) عبارت است از حاصلجمع مجموع اندازه شباهت جفتجفت عناصر یک خوشه با مجموع اندازه شباهت جفتجفت عناصر خوشه دیگر با مجموع اندازه شباهت عناصر یک خوشه با عناصر خوشه دیگر تقسیم بر مجموع تعداد عناصر دو خوشه ضرب در مجموع تعداد عناصر دو خوشه منهای یک تقسیم بر دو:
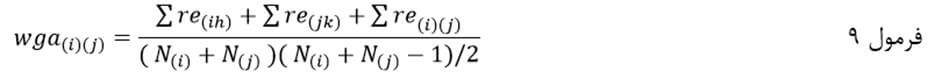
که در آن re(ih) اندازه شباهت عنصرi ام وh ام از خوشه (i) ام است. re(jk) هم اندازه شباهت عنصرj ام و k ام از خوشه (j) ام است. re(i)(j) اندازه شباهت عنصری از خوشه (i) ام با عنصری از خوشه (j) ام است. N(i) تعداد عناصر خوشه i ام است و N(j) هم تعداد عناصر خوشه (j) ام.
در این روش نیز در ابتدای خوشهبندی (مرحله صفر) هر عنصر یک خوشه به حساب میآید و ضریب متوسط درون گروهی دو خوشه همان اندازه شباهت دو عنصر است. به عنوان مثال ضریب متوسط درون گروهی خوشه (۱) با خوشه (۲) بر مبنای مجذور فاصله اقلیدسی عناصر دو خوشه (جدول ۶) عبارت است از:
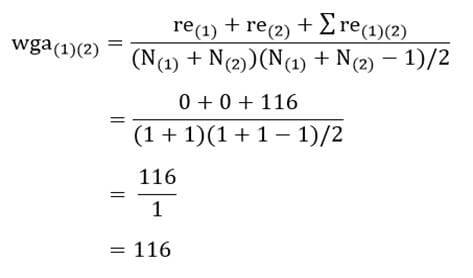
مرحله یک
در این مرحله دو خوشه (۳) و (۴) که دارای کمترین فاصله ( کمترین ضریب متوسط درون گروهی) هستند با هم ترکیب میشوند.
در اینجا ضریب متوسط درون گروهی خوشه جدید (۳و۴) با خوشه (۱) با توجه به ماتریس اندازه شباهت عناصر (جدول ۶) عبارت است از:
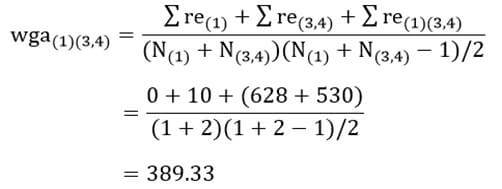
و ضریب متوسط درون گروهی خوشه (۳و۴) با خوشه (۲):
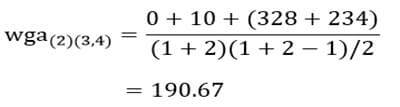
و ضریب متوسط درون گروهی خوشه (۳و۴) با خوشه (۵):
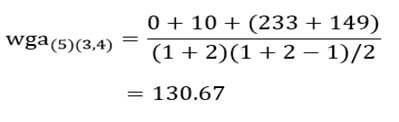
و ضریب متوسط درون گروهی خوشه (۳و۴) با خوشه (۶):
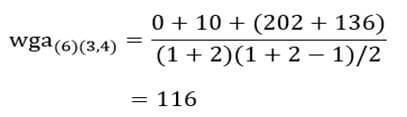
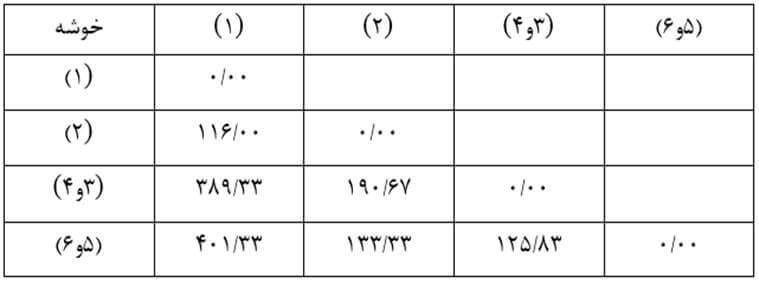
حال ماتریس فاصله خوشههای مرحله یک را تشکیل میدهیم (جدول ۱۲).

مرحله دو
در این مرحله هم دو خوشه (۵) و(۶) که دارای کمترین ضریب متوسط درون گروهی (۲۵) هستند با هم ترکیب میشوند. حال ضریب متوسط درون گروهی خوشه جدید (۵و۶) را با بقیه خوشهها احتساب کنیم.
ضریب متوسط درون گروهی خوشه (۵و۶) با خوشه (۱) با توجه به ماتریس اندازه شباهت عناصر (جدول ۶) عبارت است از:
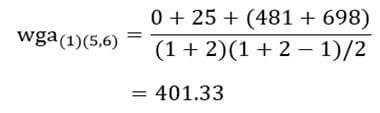
و ضریب متوسط درون گروهی خوشه (۵و۶) با خوشه (۲):
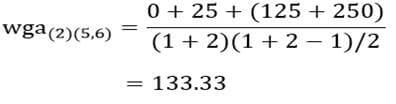
و ضریب متوسط درون گروهی خوشه (۵و۶) با خوشه (۳و۴):
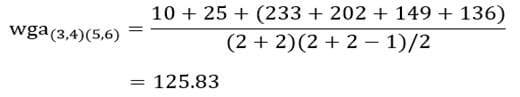
و ماتریس فاصله خوشههای مرحله دو را تشکیل میدهیم (جدول ۱۳).
مرحله سه
در این مرحله دو خوشه (۱) و(۲) را که دارای کمترین ضریب متوسط گروهی (۱۱۶) هستند با هم ترکیب میکنیم.
حال ضریب متوسط گروهی خوشه (۱و۲) با خوشه (۳و۴) با توجه به ماتریس اندازه شباهت عناصر (جدول ۶) عبارت است از:
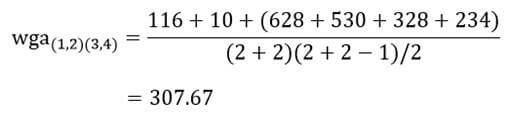
و ضریب متوسط درون گروهی خوشه (۱و۲) با خوشه (۵و۶):
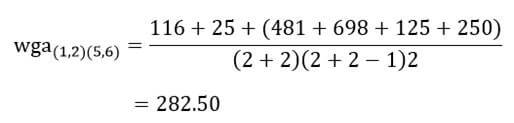
سپس ماتریس فاصله خوشههای مرحله سه را تشکیل میدهیم (جدول ۱۴).

مرحله چهار
در این مرحله دو خوشه (۳و۴) و (۵و۶) را که دارای کمترین ضریب متوسط درون گروهی (۱۲۵/۸۳) هستند با هم ترکیب میکنیم.
حال ضریب متوسط درون گروهی خوشه (۱و۲) با خوشه (۳و۴و۵و۶) با توجه به ماتریس اندازه شباهت عناصر (جدول ۶) عبارت است از:
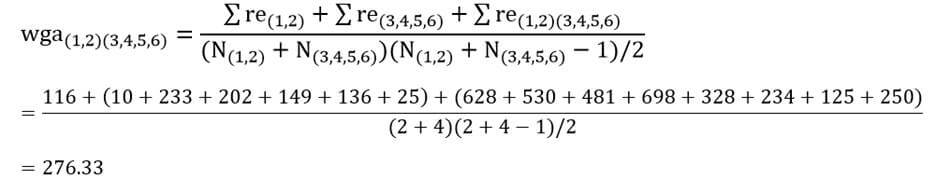
سپس ماتریس فاصله خوشههای مرحله چهار را تشکیل میدهیم (جدول ۱۵).
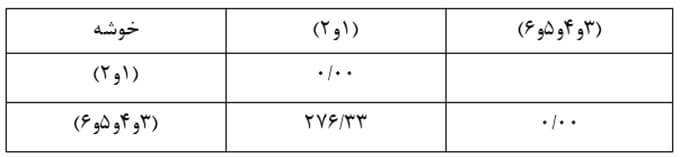
در این مرحله با ترکیب خوشه (۳و۴و۵و۶) و خوشه (۱و۲) که فاصله (ضریب متوسط درون گروهی آنها) ۲۷۶/۳۳ است به خوشه نهایی میرسیم که تمام عناصر را در برمیگیرد.
نمودار درختی ضریب متوسط درون گروهی
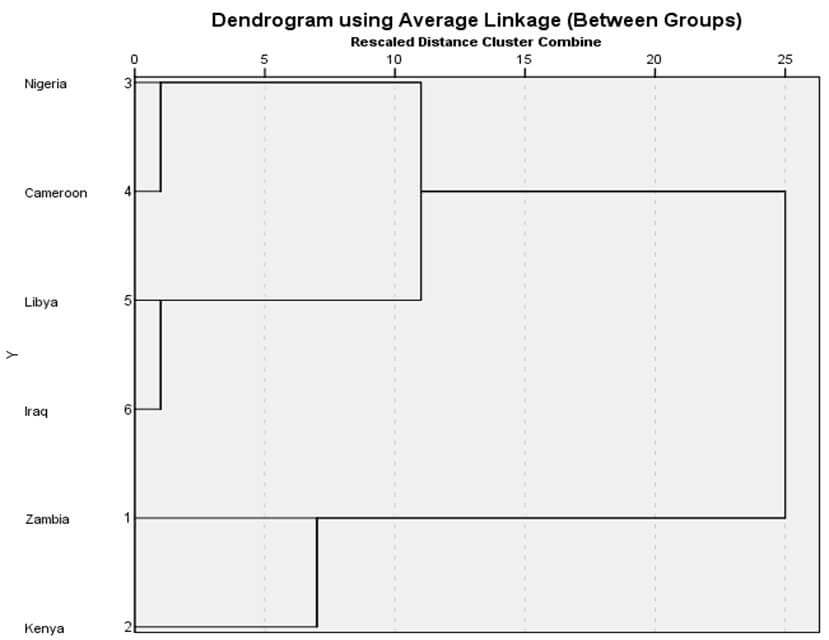
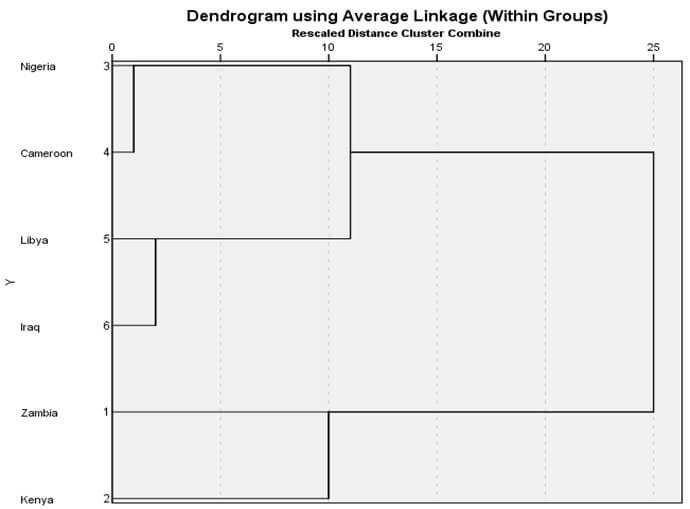
شکل ۱۰ نمودار درختی خوشهبندی با روش ضریب متوسط درون گروهی مثال ۲ است. در این نمودار درختی هم در ابتدا هر عنصری یک خوشه است. در مرحله ۱ خوشه (۱) و خوشه (۲) در فاصله ضریب متوسط درون گروهی ۱۰ با هم ترکیب شدهاند. سپس در مرحله ۲ خوشه (۵) و خوشه (۶) در فاصله ضریب متوسط درون گروهی ۲۵ با هم ترکیب شدهاند.
در مرحله ۳ خوشه (۱) و خوشه (۲) در فاصله ضریب متوسط درون گروهی ۱۱۶ با هم ترکیب شدهاند. در مرحله ۴ خوشه (۳و۴) و خوشه (۵و۶) در فاصله ضریب متوسط درون گروهی ۱۲۵/۸۳ با هم ترکیب شدهاند. سرانجام در مرحله ۵ خوشه (۳و۴و۵و۶) و خوشه (۱ و ۲) در فاصله ضریب متوسط درونگروهی ۲۷۶/۳۳ با هم ترکیب شدهاند.
تحلیل خوشه ای با روش تک اتصالی
در روش خوشهبندی تک اتصالی که روش نزدیکترین همجوار هم خوانده میشود فاصله بین خوشهها بر اساس ضریب تک اتصالی احتساب میشود. سپس دو خوشهای که دارای کمترین فاصله هستند با هم ترکیب میشوند.
در این روش خوشهبندی بر اساس بیشترین شباهت دو عنصر از دو خوشه صورت میگیرد. به بیان دیگر دو خوشه هنگامی با هم ترکیب میشوند که اندازه شباهت یک عنصر از یک خوشه با یک عنصر از خوشه دیگر از بزرگترین اندازه شباهت بین جفت عنصرهای بینخوشهای برخوردار باشد.
به این ترتیب ضریب تک اتصالی با نماد sl(i)(j) در جایی که اندازه شباهت مبتنی بر ضریب شباهت است حداکثر اندازه شباهت جفت عنصر بین خوشهای است:
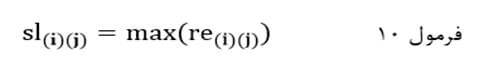
و در جایی که اندازه شباهت مبتنی بر ضریب عدم شباهت است حداقل اندازه شباهت جفت عنصر این خوشهای است:
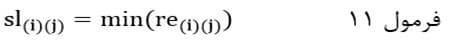
که در آن re(i)(j) اندازه شباهت جفت عنصر بین خوشهای (i) و(j) است. به عبارت دیگر re(i)(j)اندازه شباهت عنصری از خوشه (i) ام با عنصری از خوشه (j) ام است.
در ادامه عناصر مثال ۲ را با روش تک اتصالی و بر مبنای ضریب عدم تشابه مجذور فاصله اقلیدسی عناصر خوشهبندی میکنیم. از این رو مطابق فرمول ۱۱ ضریب تک اتصالی معادل حداقل ضریب عدم تشابه مجذور فاصله اقلیدسی است.
در این روش نیز در ابتدای خوشهبندی (مرحله صفر) هر عنصر یک خوشه به حساب میآید و ماتریس فاصله خوشهها بر حسب ضریب تک اتصالی (جدول ۱۶) مانند ماتریس اندازه شباهت عنصرهاست (جدول ۷) چون هر خوشه فقط یک عنصر دارد و ضریب تک اتصالی هر دو خوشه همان اندازه شباهت عنصرهای آنهاست.
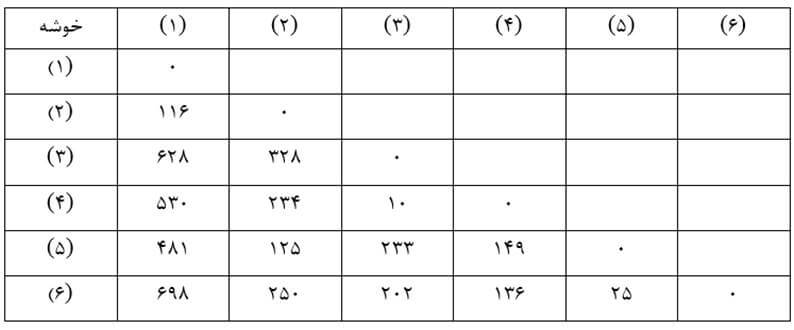
مرحله یک
در این مرحله با وارسی ماتریس فاصله خوشههای مرحله صفر (جدول۱۶) دو خوشه (۳) و (۴) را که دارای کمترین ضریب تک اتصالی (۱۰) هستند با هم ترکیب میکنیم.
حال ماتریس فاصله خوشهها بر حسب ضریب تک اتصالی مرحله یک را تشکیل میدهیم (جدول۱۷) که در آن ضریب تک اتصالی خوشه جدید (۳و۴) با بقیه خوشهها کمترین فاصله عنصر ۳ و۴ با عناصر خوشههای دیگر است. به عنوان مثال فاصله عنصر ۳ با تک عنصر خوشه (۱) معادل ۶۲۸ و فاصله عنصر ۴ با آن معادل ۵۳۰ است. بنابراین ضریب تک اتصالی خوشه (۳و۴) با خوشه (۱) کمترین آنهاست که ۵۳۰ است.
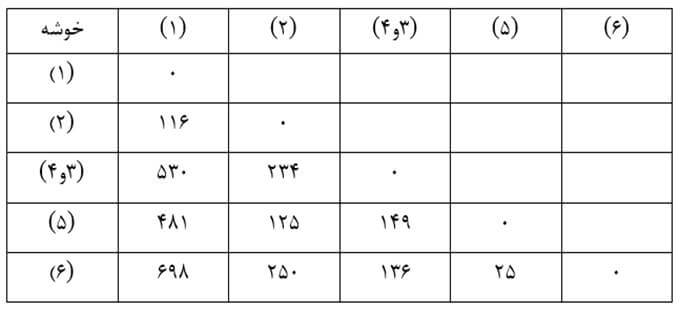
مرحله دو
در این مرحله هم دو خوشه (۵) و (۶) را که در ماتریس فاصله خوشههای مرحله یک دارای کمترین ضریب تک اتصالی (۲۵) هستند با هم ترکیب میکنیم. سپس ماتریس فاصله خوشهها بر حسب ضریب تک اتصالی مرحله دو را تشکیل میدهیم (جدول ۱۸).
مرحله سه
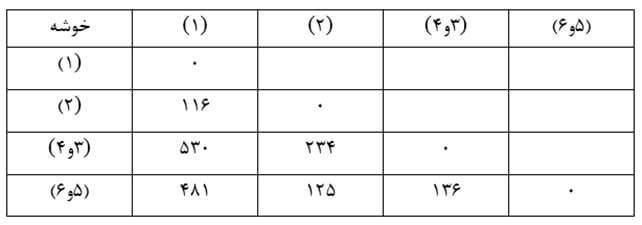
در این مرحله هم دو خوشه (۱) و (۲) را که در ماتریس فاصله خوشههای مرحله دو دارای کمترین ضریب تک اتصالی (۱۱۶) هستند با هم ترکیب میکنیم و ماتریس فاصله خوشهها بر حسب ضریب تک اتصالی مرحله سه را تشکیل میدهیم (جدول ۱۹).
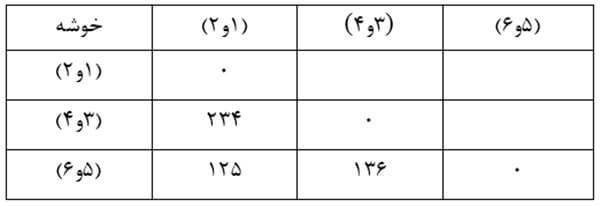
مرحله چهار
در این مرحله هم دو خوشه (۱و۲) و (۵و۶) را که در ماتریس فاصله خوشهها بر حسب ضریب تک اتصالی مرحله سه دارای کمترین ضریب تک اتصالی (۱۲۵) هستند با هم ترکیب میکنیم و ماتریس فاصله خوشهها بر حسب ضریب تک اتصالی مرحله چهار را تشکیل میدهیم (جدول ۲۰).

در این مرحله با ترکیب خوشه (۱و۲و۵و۶) و خوشه (۳و۴) که فاصله (ضریب تک اتصالی) آنها در مرحله چهار ۱۳۶ است به خوشه نهایی میرسیم که تمام عناصر را در بر میگیرد.
نمودار درختی تک اتصالی
شکل ۱۱ نمودار درختی خوشهبندی با روش تک اتصالی مثال ۲ است. در این نمودار درختی هم در ابتدا هر عنصری یک خوشه است. در مرحله ۱ خوشه (۳) و خوشه (۴) در فاصله ۱۰ با هم ترکیب شدهاند. سپس در مرحله ۲ خوشه (۵) و خوشه (۶) در فاصله ۲۵ با هم ترکیب شدهاند. در مرحله ۳ هم خوشه (۱) و خوشه (۲) در فاصله ۱۱۶ با هم ترکیب شدهاند. در مرحله ۴ نیز خوشه (۱و۲) و خوشه (۵و۶) در فاصله ۱۲۵ با هم ترکیب شدهاند. سرانجام در مرحله ۵ خوشه (۱و۲و۵و۶) و خوشه (۳و۴) در فاصله ۱۳۶ با هم ترکیب شدهاند.
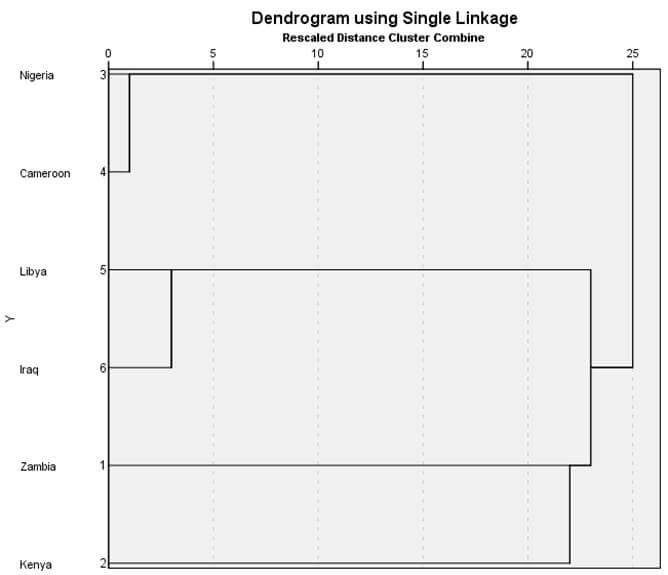
تحلیل خوشه ای با روش تام اتصالی
در روش خوشهبندی تام اتصالی که روش دورترین همجوار هم خوانده میشود فاصله خوشهها بر اساس ضریب تام اتصالی احتساب میشود. سپس دو خوشهای که دارای کمترین فاصله هستند با هم ترکیب میشوند.
ضریب تام اتصالی دو خوشه هم بزرگترین اندازه شباهت بین جفت عنصرهای بین خوشهای آنهاست. به بیان دیگر فاصله دو خوشه دورترین فاصله عنصری از یک خوشه با عنصری از خوشه دیگر است.
به این ترتیب ضریب تام اتصالی با نماد cl(i)(j) درجایی که اندازه شباهت مبتنی بر ضریب شباهت است حداقل اندازه شباهت جفت عنصر بین خوشهای است:
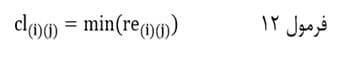
و در جایی که اندازه شباهت مبتنی بر ضریب عدم شباهت است حداکثر اندازه شباهت جفت عنصر بین خوشهای است:
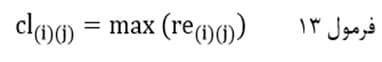
که در آن re(i)(j) اندازه شباهت جفت عنصر بین خوشهای (i) و (j) است. به بیان دیگر re(i)(j) اندازه شباهت عنصری از خوشه (i) ام با عنصری از خوشه (j) ام است.
در ادامه عناصر مثال ۲ را با روش تام اتصالی و بر مبنای ضریب عدم تشابه مجذور فاصله اقلیدسی عناصر خوشهبندی میکنیم. از این رو مطابق فرمول ۱۳ ضریب تام اتصالی معادل حداکثر مجذور فاصله اقلیدسی است.
در این روش نیز در ابتدای خوشهبندی (مرحله صفر) هر عنصر یک خوشه به حساب میآید و ماتریس فاصله خوشهها بر حسب ضریب تام اتصالی (جدول ۲۱) مانند ماتریس اندازه شباهت عنصرهاست (جدول ۶) چه هر خوشه فقط یک عنصر دارد و ضریب تام اتصالی هر دو خوشه همان اندازه شباهت عنصرهای آنهاست.
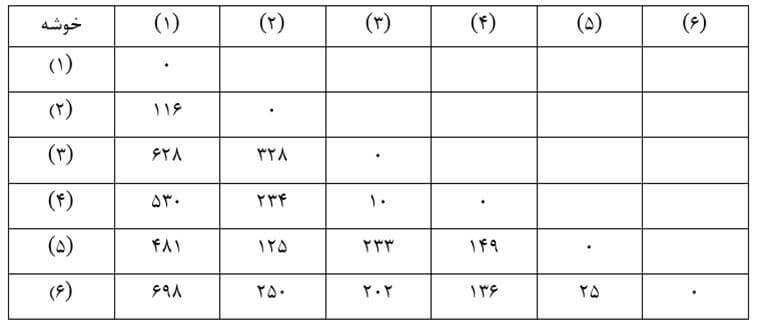
در این مرحله با وارسی ماتریس فاصله خوشهها بر حسب ضریب تام اتصالی مرحله صفر (جدول ۲۱) دو خوشه (۳) و (۴) را که دارای کمترین ضریب تام اتصالی (۱۰) هستند با هم ترکیب میکنیم.
حال ماتریس فاصله خوشهها بر حسب ضریب تام اتصالی مرحله یک را تشکیل می دهیم (جدول ۲۲) که در آن ضریب تام اتصالی خوشه جدید (۳و۴) با بقیه خوشهها بزرگترین فاصله عنصر ۳ و ۴ با عناصر خوشههای دیگر است. به عنوان مثال فاصله عنصر ۳ با تک عنصر خوشه (۱) معادل ۶۲۸ و فاصله عنصر ۴ با آن معادل ۵۳۰ است. بنابراین ضریب تام اتصالی خوشه (۳و۴) با خوشه (۱) بزرگترین آنهاست که ۶۲۸ است.
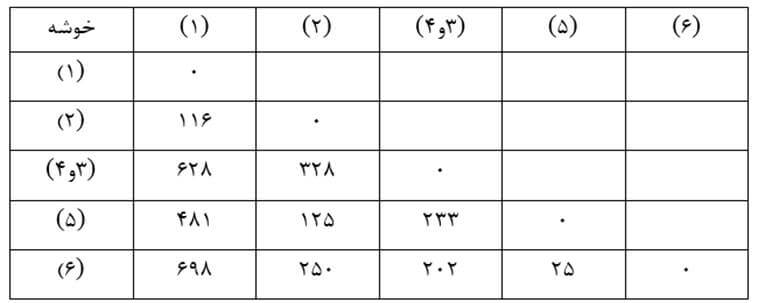
مرحله دو
در این مرحله هم دو خوشه (۵) و (۶) را که در ماتریس فاصله خوشههای مرحله یک دارای کمترین فاصله (۲۵) هستند با هم ترکیب میکنیم. سپس ماتریس فاصله خوشههای مرحله دو را تشکیل میدهیم (جدول ۲۳) که در آن ضریب تام اتصالی خوشه جدید (۵و۶) با بقیه خوشهها بزرگترین فاصله عنصر ۵ و۶ با عناصر خوشههای دیگر است.
به عنوان مثال فاصله عنصر ۵ این خوشه با عنصر ۳ خوشه (۳ و۴) معادل ۲۳۳ و با عنصر ۴ آن معادل ۱۴۹ است و فاصله عنصر ۶ این خوشه با عنصر ۳ خوشه (۳ و۴) معادل ۲۰۲ و با عنصر ۴ آن معادل ۱۳۶ است. در نتیجه ضریب تام اتصالی خوشه جدید (۵ و۶) با خوشه (۳ و۴) معادل ۲۳۳ است که بزگترین فاصله بین چهار فاصله میان عناصر آن دو خوشه است.
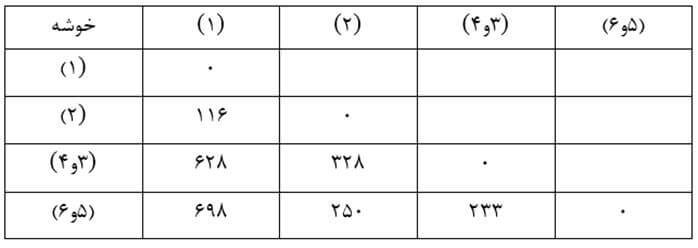
مرحله سه
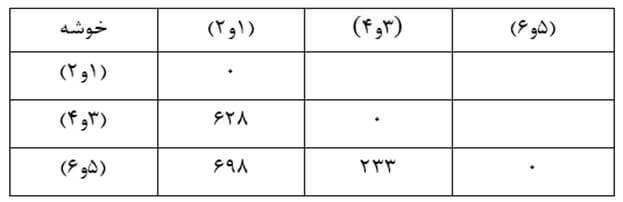
در این مرحله هم دو خوشه (۱) و (۲) را که در ماتریس فاصله خوشههای مرحله دو دارای کمترین فاصله (۱۱۶) هستند با هم ترکیب میکنیم و ماتریس فاصله خوشههای مرحله سه را تشکیل میدهیم (جدول ۲۴).
مرحله چهار
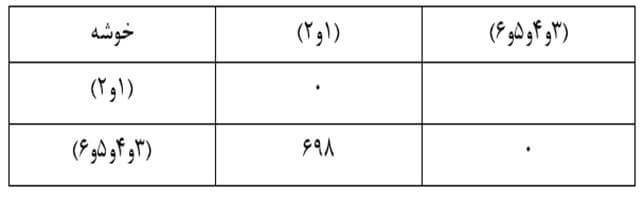
در این مرحله دو خوشه (۳و۴) و (۵و۶) را که در ماتریس فاصله خوشههای مرحله سه دارای کمترین فاصله (۲۳۳) هستند با هم ترکیب میکنیم و ماتریس فاصله خوشههای مرحله چهاررا تشکیل میدهیم (جدول ۲۵).
مرحله پنج
در این مرحله با ترکیب دو خوشه (۳و۴و۵و۶) و (۱و۲) که فاصله آنها ۶۹۸ است به خوشه نهایی میرسیم که تمام عناصر را دربر میگیرد.
نمودار درختی تام اتصالی
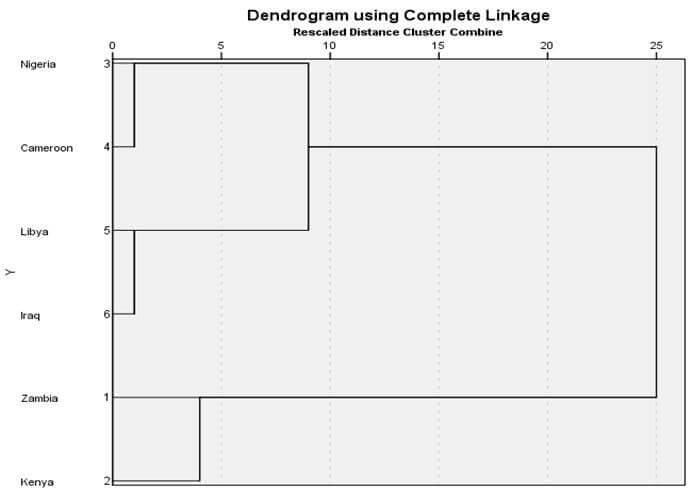
شکل ۱۲ نمودار درختی خوشهبندی با روش تام اتصالی مثال ۲ است. در این نمودار درختی هم در ابتدا هر عنصری یک خوشه است. در مرحله ۱ خوشه (۳) وخوشه (۴) در فاصله ۱۰ با هم ترکیب شدهاند. سپس در مرحله ۲ خوشه (۵) و خوشه (۶) در فاصله ۲۵ باهم ترکیب شدهاند. در مرحله ۳ هم خوشه (۱) و خوشه (۲) در فاصله ۱۱۶ با هم ترکیب شدهاند. در مرحله ۴ خوشه (۳ و ۴) و خوشه (۵ و ۶) در فاصله ۲۳۳ با هم ترکیب شدهاند. سرانجام در مرحله ۵ خوشه (۳ و ۴ و ۵ و ۶) و خوشه (۱ و ۲) در فاصله ۶۹۸ با هم ترکیب شدهاند.
تحلیل خوشه ای به روش وارد
در روش خوشهبندی وارد که عنوان اختصاری روش خوشهبندی حداقل واریانس وارد است و اتصال وارد هم خوانده میشود در هر مرحله خوشهبندی فاصله بین خوشهها براساس ضریب وارد احتساب میشود که ضریب مجذور انحرافات مقادیر عناصر درون خوشهها از میانگین متغیرهاست. سپس دو خوشهای که دارای کمترین فاصله هستند با هم ترکیب میشوند.
ضریب وارد با نماد E(i)(j) عبارت است از مجموع مجذور انحراف مقادیر از میانگین متغیر در درون دو خوشه (i) و (j) به اضافه مجموع مجذور انحراف مقادیر از میانگین متغیر در درون تک تک خوشههای دیگر:
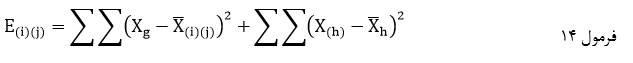
که در آن Xg مقدار عنصر g ام دو خوشه (i) و (j) در متغیر X است و ![]() میانگین متغیر X در آن دو خوشه Xh هم مقدار عنصر h ام خوشه (h) در متغیرX است و
میانگین متغیر X در آن دو خوشه Xh هم مقدار عنصر h ام خوشه (h) در متغیرX است و ![]() میانگین متغیر X در خوشه (h).در این روش نیز در ابتدای خوشهبندی (مرحله صفر) هرعنصر یک خوشه به حساب میآید.
میانگین متغیر X در خوشه (h).در این روش نیز در ابتدای خوشهبندی (مرحله صفر) هرعنصر یک خوشه به حساب میآید.
مرحله یک
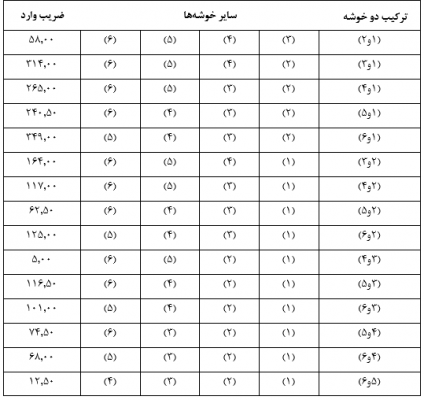
در این مرحله هربار دو خوشه را در نظر میگیریم و ضریب وارد را که مبین فاصله دو خوشه است حساب میکنیم. به عنوان مثال با توجه به اینکه میانگین دو خوشه (1) و (2) در متغیر X1 معادل 50 و در متغیر X2 معادل 71 است و میانگین سایر خوشهها نیز که تکعنصری هستند در هر متغیر معادل مقدار تک عنصر است ضریب وارد دو خوشه (1) و (2) عبارت است از:
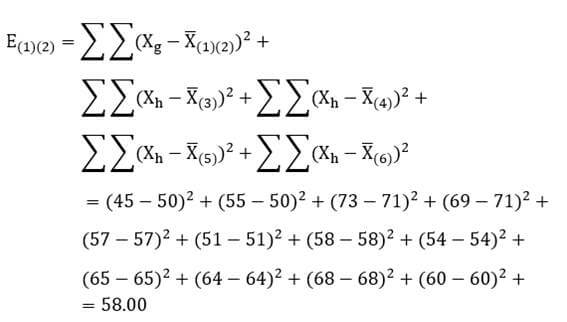
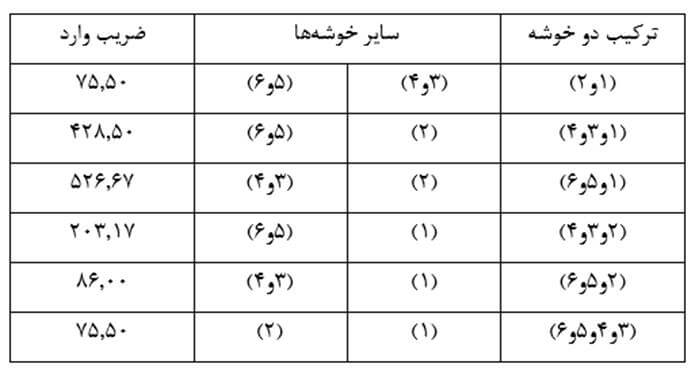
با همین روال ضریب وارد تمام دو خوشههای ممکن را حساب میکنیم (جدول ۲۶). سپس دو خوشهای که دارای کمترین فاصله (کمترین ضریب وارد) هستند با هم ترکیب میشوند. در این مثال با وارسی جدول ۲۶ میبینیم ترکیب دو خوشه (۳) و (۴) از کمترین ضریب وارد برخوردار است. پس این دو خوشه را با هم ترکیب میکنیم.
مرحله دو
در این مرحله نیز هربار دو خوشه را در نظر میگیریم و ضریب وارد آن دو خوشه را حساب میکنیم. به عنوان مثال با توجه به اینکه میانگین دو خوشه (1) و (2) در متغیر X1 معادل 50 و در متغیر X2 معادل 71 است و میانگین خوشه (3 و 4) در متغیر X1 معادل 57/5 و در متغیر X2 معادل 52/5 است و میانگین سایر خوشهها نیز که تکعنصری هستند در هر متغیر همان مقدار تک عنصر است ضریب وارد ترکیب دو خوشه (1) و (2) عبارت است از:
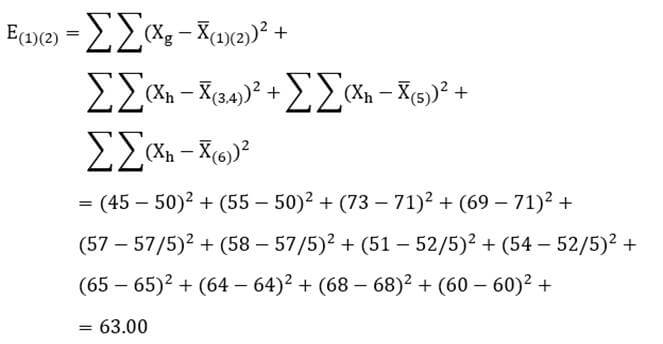
با همین روال ضریب وارد ترکیب تمام دو خوشههای ممکن را حساب میکنیم ( جدول ۲۷). سپس دو خوشهای که دارای کمترین فاصله (کمترین ضریب وارد) هستند با هم ترکیب میشوند. در این مثال با وارسی جدول ۲۷ میبینیم ترکیب دو خوشه (۵) و (۶) از کمترین ضریب وارد برخوردار است. بنابراین دو خوشه را با هم ترکیب میکنیم.
مرحله سه
در این مرحله هم باز هر بار دو خوشه را در نظر میگیریم و ضریب وارد آن دو خوشه را حساب میکنیم. به عنوان مثال با توجه به اینکه میانگین دو خوشه (1) و (2) در متغیر X1 معادل 50 و در متغیر X2 معادل 71 است و میانگین خوشه (3 و 4) در متغیر X1 معادل 57/5 و در متغیر X2 معادل 52/5 است و میانگین خوشه (5 و 6) در متغیر X1 معادل 66/5 و در متغیر X2 معادل 62 است ضریب وارد ترکیب دو خوشه (1) و (2) عبارت است از:
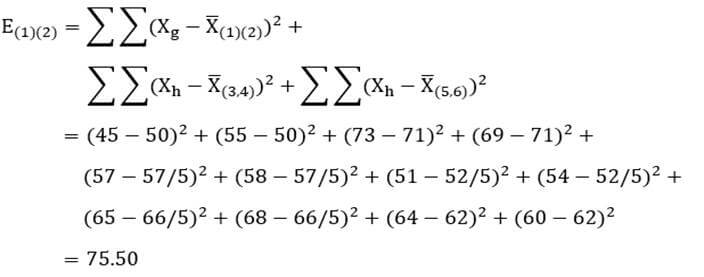
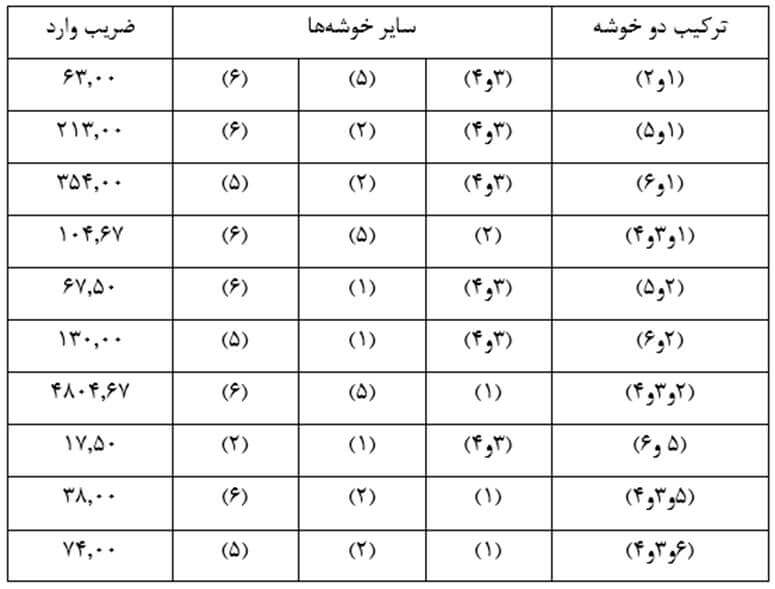
با همین روال ضریب وارد تمام دو خوشههای ممکن را حساب میکنیم (جدول ۲۸). در این مثال دو خوشه (۱) و (۲) و همچنین دو خوشه (۳ و ۴) و (۵ و ۶) از کمترین ضریب وارد برخوردارند. از این رو یکی از این جفت خوشهها را و معمولا کم عنصر ترین خوشهها را که دو خوشه (۱) و (۲) هستند با هم ترکیب میکنیم.
مرحله چهار
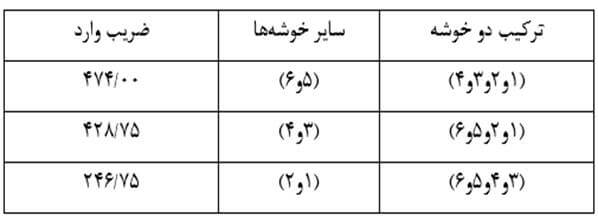
در این مرحله هم باز هر بار دو خوشه را در نظر میگیریم و ضریب وارد دو خوشه را حساب میکنیم (جدول ۲۹). در این مثال با وارسی جدول ۲۷ میبینیم ترکیب دو خوشه (۳ و ۴) و (۵ و ۶) از کمترین ضریب وارد برخوردار است. بنا بر این دو خوشه را با هم ترکیب میکنیم.
مرحله پنج
در این مرحله با ترکیب دو خوشه (۳ و ۴ و ۵ و ۶) و (۱ و ۲) که فاصله (ضریب وارد) آنها ۸۳۳/۶۹۰ است به خوشه نهایی میرسیم که تمام عناصر را در بر میگیرد.
نمودار درختی وارد
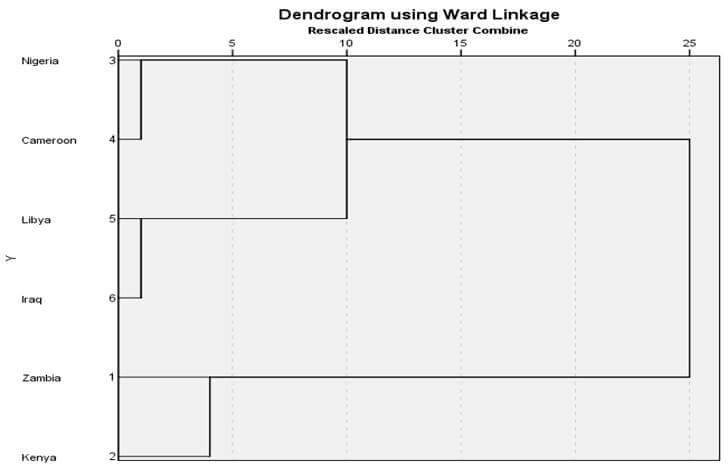
شکل ۱۳ نمودار درختی خوشهبندی با روش وارد مثال ۲ است. در این نمودار درختی هم در ابتدا هر عنصری یک خوشه است. در مرحله ۱ خوشه (۳) و خوشه (۴) در فاصله۵/۰۰ باهم ترکیب شدهاند. سپس در مرحله ۲ خوشه (۵) و خوشه (۶) در فاصله ۱۷/۵۰ با هم ترکیب شدهاند. در مرحله ۳ هم خوشه (۱) و خوشه (۲) در فاصله ۷۵/۵۰ با هم ترکیب شدهاند. در مرحله ۴ خوشه (۳ و ۴) و خوشه (۵ و ۶) در فاصله ۲۴۶/۷۵ با هم ترکیب شدهاند. سرانجام در مرحله ۵ خوشه (۳ و ۴ و ۵ و ۶) و خوشه (۱ و ۲) در فاصله ۶۹۰/۸۳۳ با هم ترکیب شدهاند.
برگرفته از وب سایت آمار پیشرو
