آزمون مک نمار
آزمون مک نمار یک آزمون ناپارامتری است که اغلب در مورد داده های اسمی دو مقوله ای یا دوپاسخی مربوط به دو نمونه ی مرتبط یا همبسته به کار می رود. این آزمون به ویژه در مواردی به کار می رود که می خواهیم نظرهای یا عملکردهای قبلی یا بعدی موردها (معمولا افراد) را با هم مقایسه کنیم.
WWW.rava20.ir
مثالی برای آزمون مک نمار:
فرضیه تحقیق: نسبت معلمان متمایل به ادامه خدمت در آ. پ پس از خدمت 30 سالگی پیش از برگزاری جلسه توجیهی با این نسبت پس از برگزاری جلسه توجیهی کم تر است.
H0= πpre= πpast H1 = πpre< πpost
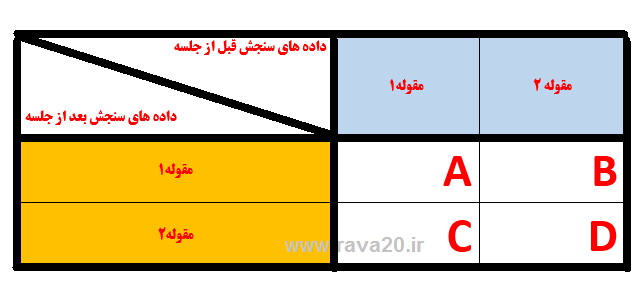
محقق پیش از جلسه توجیهی میزان تمایل معلمان به ادامه خدمت در آ.پ پس از 30 سال خدمت مورد سنجش قرار می دهد و درصد افرادی که تمایل دارند یا ندارند را مشخص می کند و پس از آن جلسه ای توجیهی در رابطه با مزایای استمرار خدمت پس از 30 سال خدمت برگزار می کند و دوباره میزان تمایل افراد را مورد سنجش قرار می دهد و درصد ها را مشخص می کند. در اینجا باید مشخص شود کسی که قبل از جلسه نظرش مثت یا منفی بوده، بعد از جلسه توجیهی جه نظری دارد.
آزمون مک نمار به افرادی که تغییر عقیده یا عملکرد نداده اند، یعنی مقادیر a وd اهمیت نمی دهد و تنها با مقادیری سروکار دارد که با تغییر عقیده مربوط می شوند یعنی b وc. منطق اصلی انجام این آزمون این است که اگر تدبیر یا عامل مورد نظر که پس از سنجش اول اعمال می شود مؤثر نباشد، می بایست یا در عقیده ها و عملکردها تغییری صورت نگیرد و یا تغییر در میان آزمودنی ها به سوی یکی از طرف ها (مثبت یا منفی، مخالف یا موافق و…) برابر با طرف دیگر باشد. بنابراین فرضیه پژوهش در این آزمون بیان می دارد که بین دو دسته از داده ها تفاوت معناداری ایجاد می شود.
آماره ی آزمون مک نمار به صورت زیر تعریف می شود :
χ^2=(|b-c|-1)^2/(b+c)
در این آزمون معناداری آماری با ارزیابی احتمال کای دو فوق و با استفاده از جدول توزیع کای دو تعیین می گردد. معنی داری آماری نشان می دهد که فراوانی یا احتمال های مشاهده شده به صورت همگنی نیستند و تفاوت معنی داری بین آن ها وجود دارد. چنانچه مقدار آماره از مقدار حاصل از جدول توزیع کای دو بزرگتر باشد فرضیه صفر پذیرفته نمی شود.
نکته : وقتی مقادیر bیا c کوچک باشند، آزمون مک نمار به خوبی با توزیع کای دو منطبق نمی شود و بنابراین گفته می شود که جمع bوc حداقل باید 10 یا بیشتر باشد.
www.rava20.ir