مقدار T-Value و مقدار P-Value در آزمون فرض آماری چیست؟

1- مفدمه بر آزمون فرض آماری
مطابق با الزامات استانداردهای ISO 15189:2022 و ISO/IEC 17025:2017 آزمایشگاه باید یک روش اجرایی برای پایش اعتبار نتایج، داشته باشد.
دادههای به دست آمده باید به نحوی ثبت شوند که روند آنها قابل تشخیص باشد.
در جایی که قابل اجرا است از فنون آماری در بازنگری نتایج استفاده شود.
در بسیاری از مراکز آزمایشگاهی از آزمونهای فرض آماری برای کنترل کیفیت نتایج آزمون، تحلیل نتایج مقایسات بین آزمایشگاهی و یا صحه گذاری روشهای آزمون برای برآوزدهسازی الزامات استاندارد ایزو 17025 و استاندارد ایزو 15189 استفاده میشود.
اگر کارکنان آزمایشگاه و یا پژوهشگران با علم آمار آشنایی نداشته باشند و به دنبال استفاده از از نرم افزارهای آماری مانند minitab, spss و … برای تجزیه و تحلیل نتایج خود باشند، در مواجه با خروجیهای این نرم افزارها احساسی شبیه احساس آلیس در سرزمین عجایب را پیدا خواهند کرد.
ناگهان آنها با یک دنیا فانتزی که در آن عبارات عجیب و مرموزی وجود دارد، روبه رو میشوند.
به عنوان مثال ظهور مقادیر T و P را در انجام آزمون فرض t-test را در نظر بگیرید.
در مشاهد این خروجی شما ممکن است بسیار متعجب شوید!!

این مقادیر واقعاً چیست؟
آنها از کجا بدست آمدهاند؟
حتی اگر شما از مقدار P-value برای تفسیر آماری نتایج خود به دفعات بسیار زیاد استفاده کرده باشید، باز هم ممکن است منشا واقعی آن ممکن هنوز برای شما گنگ باشد.
2- مقادیر P value و t-value در آزمون T-Test
مقدار P value و مقدار t-value به طور جدایی ناپذیری با هم مرتبط است.
آنها به صورت خیلی مشابه در کنار هم نتایج تجزیه و تحلیل آماری ظاهر میشوند.
هنگامی که شما آزمون t-test را انجام میدهید، معمولا برای پیدا کردن شواهدی از یک اختلاف معنی داری در میان دو جمعیت (۲-sample t) و یا بین یک جمعیت مقدار هدف (۱-sample t) هستید.
به عنوان مثال در مقایسه بین آزمایشگاهی به دنبال آن هستیم که ببینم نتایج بدست آمده در دو آزمایشگاه مختلف بر روی یک نمونه یکسان بایکدیگر اختلاف معناداری دارند یا نه؟
مقدار t اندازه تفاوت را نسبت به تغییرپذیری بدست آمده از نمونهها را میسنجد.
به عبارت دیگر، T برابر با تفاوت محاسبه شده تقسیم بر خطای استاندارد (SE MEAN) است.
هر چه مقدار T (چه در جهت مثبت و چه در جهت منفی) بزرگتر باشد احتمال بیشتری برای رد فرض صفر به وجود خواهد آمد و هر چه مقدار T به صفر نزدیکتر باشد احتمال بیشتری برای پذیرش فرض صفر وجود خواهد داشت. (فرض صفر یعنی تفاوت معنیداری وجود ندارد.)
بخاطر داشته باشید که مقدار t که در خروجی نرم افزار نشان داده شده است بر اساس تنها یک نمونه که به صورت تصادفی از کل جمعیت گرفته شده، محاسبه می گردد و اگر نمونهبرداری تصادفی را مجدداً انجام دهید ممکن است مقدار t کمی متفاوت از آنچه قبلا محاسبه کردهاید، بدست آید.
حال این سئوال مطرح میشود که در بسیاری از نمونه های که به صورت تصادفی از یک جمعیت یکسان گرفته میشود، چقدر تفاوت در مقدار t انتظار داریم که به وجود آید؟
و چگونه مقدار t بدست آمده از داده های مربوط به نمونه خود را نسبت به مقدار t مورد انتظار مقایسه کنیم؟
این کار را میتوان با رسم یک توزیع t انجام داد.
3- استفاده از یک تابع توزیع t برای محاسبه احتمال
به عنوان مثال فرض کنید که با استفاده از یک آزمون فرض آماری به روش ۱-sample t-test می خواهید تعیین کنید که یک ویژگی در جمعیت مورد مطالعه بزرگتر از یک مقدار مشخص میباشد یا خیر؟
در این مثال مقدار مشخص ۵ در نظر گرفته شده که از یک نمونه با ۲۰ مشاهده بدست آمده است.
همانطور که در شکل بالا نشان داده شده مقدار t در خروجی نرم افزار minitab برابر با ۲٫۸ بدست آمده است.
لذا میخواهیم ببینم در یک تابع توزیع T با درجه آزادی ۱۹ (درجه آزادی برابر است با تعداد مشاهدات منهای یک) احتمال آنکه مقدار t برابر با ۲٫۸ شود چقدر است.
برای انجام این کار از نرم افزار minitab می توان استفاده نمود بدین منظور در این نرم افزار مسیر زیر را طی می کنیم:
In Minitab, choose Graph > Probability Distribution Plot.
Select View Probability, then click OK.
From Distribution, select t.
In Degrees of freedom, enter ۱۹.
Click Shaded Area. Select X Value. Select Right Tail.
In X Value, enter 2.8 (the t-value), then click OK.
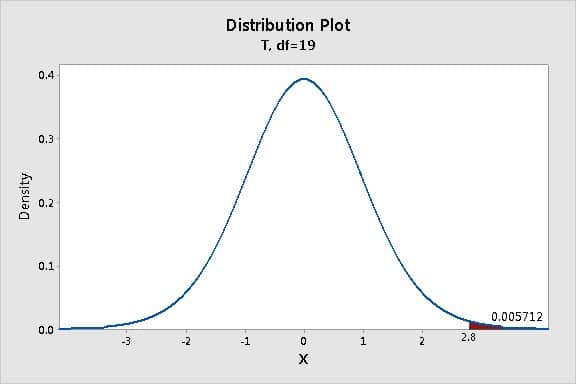
بیشترین مقدار مورد انتظار برای t محلی است که قله گراف بالا قرار دارد (یعنی مقدار صفر). این بدان معنا است که در بیشتر واقع انتظار میرود که مقدار t=0 شود.
علت این امر آن است که وقتی یک نمونه به صورت تصادفی از یک جامعه برداشته می شود انتظار می رود که اختلافی بین میانگین نمونه با میانگین جامعه وجود نداشته باشد یعنی به احتمال زیاد اختلاف بین میانگین نمونه و میانگین جامعه نزدیک به صفر است.
4- مجاسبه مقدار T-Value و مقدار P-Value
احتمال اینکه مقدار T-value (چه در جهت مثبت و چه در جهت منفی) در آزمونهای فرض آماری مقدار بزرگی شود خیلی کم است. یعنی آنکه هر چه از مقدار صفر در هر دو جهت دور می شویم احتمال رخداد چنین وضعیتی به صورت طبیعی کاهش می یابد. به عنوان مثال ناحیه قرمز مشخص شده در منحی فوق احتمال اینکه مقدار T-Value برابر با ۲٫۸ و بیشتر از آن باشد را نشان میدهد. احتمال این امر ۰٫۰۰۵۷۱۲ محاسبه شده است که اگر آن را گرد کنیم برابر با ۰٫۰۰۶ می شود که به این مقدار P-Value گفته می شود.
به عبارت دیگر، احتمال به دست آوردن T-Value برابر با ۲٫۸ و یا بالاتر، زمانی که نمونه برداری از جمعیت یکسان (در مثال، یک جمعیت با میانگین ۵ در نظر گرفته شده)، حدود ۰٫۰۰۶ است.
چقدر احتمال این رخ داد وجود دارد؟ این رخداد مثل آن است که در برداشت تصادفی از ۵۲ برگ در بازی پوکر ۲ برگ تک پشت سر هم به دست شما برسد. شناس چنین رخدادی بسیار کم است!!

این امر که این نمونه از جامعهی با میانگین بیشتری از مقدار مشخص شده (در این مثال ۵) باشند، محتمل تر است. بعبارت دیگر: از آنجا که مقدار P-value بسیار کوچک تر از (< alpha level) است، شما فرض صفر رد و نتیجه گیری است که تفاوت معنی داری وجود دارد.
مقادیر T و P به طور جدایی ناپذیری مرتبط هستند و به سادگی میتوانید از آنها برای تصمیم در خصوص درست یا نادرست بودن یک فرض استفاده کنید. مقدار یکی از آنها بدون تغییر در دیگری، تغییر نخواهد کرد. مقادیر بزرگتر قدرمطلق T-Value منجر به مقادیر کوچکتر P-value میشود که امر سبب کاهش احتمال پذیرش فرض صفر میشود. به طور معمول مطالعات آماری در سطح اطمینان ۹۵% (یعنی آلفای برابر با ۰٫۰۵) انچام میشود.
در سطح اطمینان ۹۵% اگر P-value کوچکتر یا مساوی ۰٫۰۵ باشد فرض صفر را رد میکنند و در غیر این صورت فرض صفر را نمی توان رد کرد.
5- سخن پایانی
نکته آخر اینکه که در برخی از نرم افزارها مانند spss مقدار p-value در جدول های خروجی نرم افزار تحت عنوان Significant Level ذکر میشود. در این پست آموزشی برخی از نکات مهم برای در خصوص آزمون فرض T-TEST و مقدار P-Value ذکر شود.
- برای مشاهده لیست همه ی پرسشنامه های استاندارد لطفا همین جا روی پرسشنامه استاندارد کلیک فرمایید.
- تحلیل داده های آماری برای پایان نامه و مقاله نویسی ،تحلیل داده های آماری شما با نرم افزارهای کمی و کیفی ،مناسب ترین قیمت و کیفیت عالی انجام می گیرد.نرم افزار های کمی: SPSS- PLS – Amosنرم افزار کیفی: Maxqudaتعیین حجم نمونه با:Spss samplepower
- روش های تماس:Mobile : 09143444846 واتساپ – تلگرام کانال
- تلگرام سایت: برای عضویت در کانال تلگرام سایت اینجا کلیک کنید(البته قبلش فیلتر شکن روشن شود!!) مطالب جالب علمی و آموزشی در این کانال درج می گردد.
