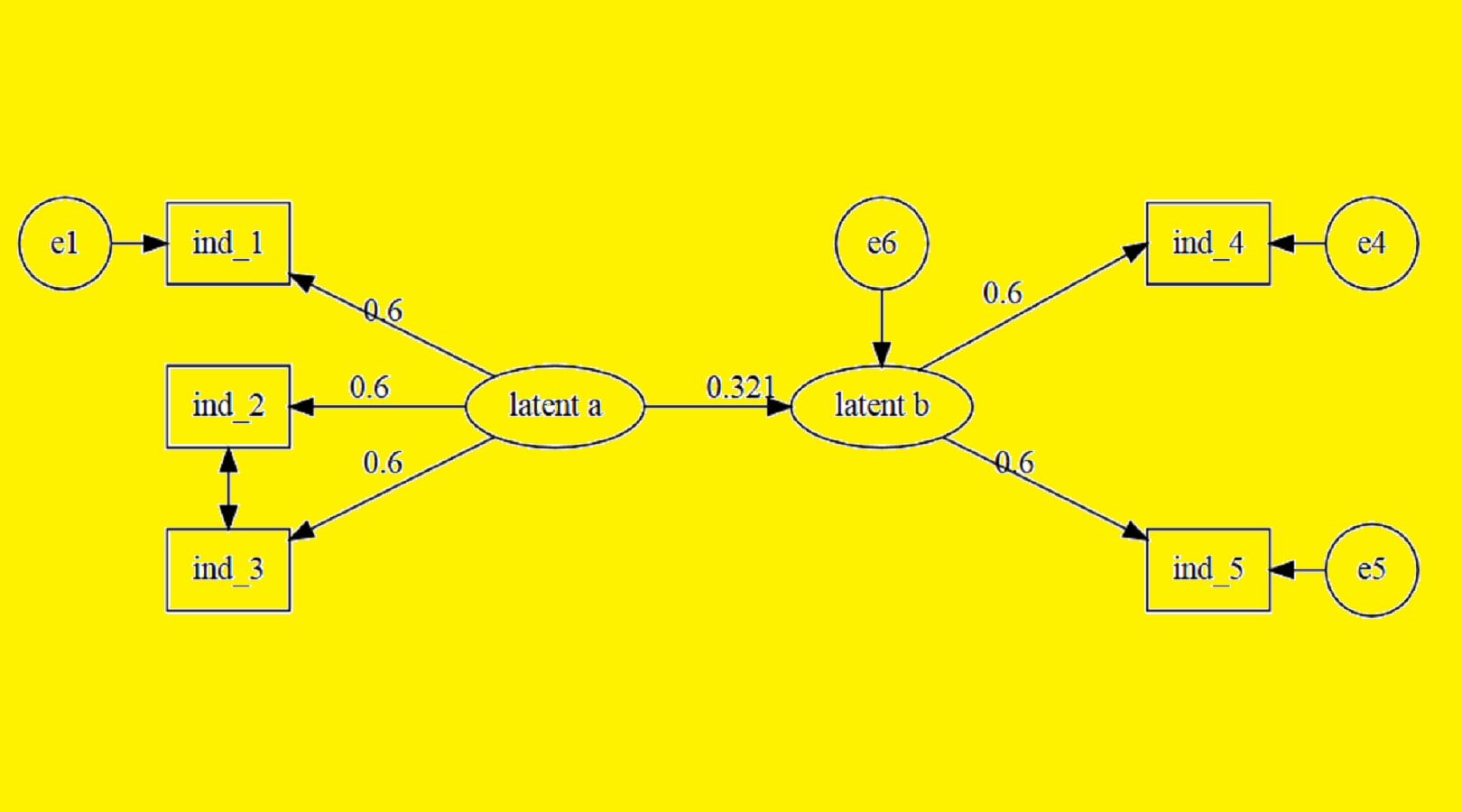
مدل معادلات ساختاری (Structural Equation Modeling) — مفاهیم، روش‌ها و کاربردها

«مدل معادلات ساختاری» (Structural Equation Modeling)،‌ ابزاری قدرتمند در تحلیل‌های چند متغیره آماری محسوب می‌شود. این روش که به اختصار SEM نیز نامیده می‌شود، از روش‌هایی که در تحلیل چند متغیره وجود دارد در حالت خاص استفاده کرده و مدل‌هایی مناسب برای داده‌هایی مربوط به تحقیقات کیفی ارائه می‌دهد.

 کاربرد مدل معادلات ساختاری

در SEM از مفاهیم ساده‌ای مانند واریانس و کوواریانس به عنوان معیارهایی برای اندازه‌گیری پراکندگی یا وابستگی بین متغیرها استفاده کرده و مدل مناسب با داده‌ها با کمترین متغیر یا ایجاد متغیرهای جدید، تولید می‌شود.

از کاربردهای مهم مدل معادلات ساختاری می‌توان به موارد زیر اشاره کرد:

1. «تحلیل مسیر» (Path Analysis) یا مدلی که  رابطه بین متغیرها را نشان می‌دهد.
2. «تحلیل عاملی تاییدی» (Confirmatory Factor Analysis) که شبیه تحلیل عاملی است و آزمون‌های مربوط به وزن عامل (ضریب هر عامل) و همبستگی درونی را انجام می‌دهد.
3. «تحلیل عاملی مرتبه دوم» (Second Order Factor Analysis) که در آن ماتریس همبستگی عوامل، خود قابل تجزیه به عوامل دیگری است که «عوامل ثانویه» (Second Order Factors) خوانده می‌شوند.
4. «مدل تحلیل رگرسیونی» (Regression Models)،‌ که از رگرسیونی خطی استفاده کرده و با منظور تخصیص وزن به هر یک از متغیرها، مدل کمترین مربعات خطا را می‌سازد.
5. «مدل ساختار کوواریانس» (Covariance Structure Models) که به بررسی ساختار و شکل ماتریس کوواریانس می‌پردازد و در مورد آن آزمون فرض انجام می‌دهد.
6. «مدل ساختار همبستگی» (Correlation Structure Models)، که آزمون‌های فرض مربوط به ساختار ماتریس همبستگی را محاسبه می‌کند.

با توجه به گزینه‌هایی زیادی که معادلات ساختاری با آن مواجه است، تفکیک و تعریف دقیق آن به آسانی میسر نیست. آنچه اهمیت دارد، ابزارهایی است که SEM از آن‌ها بهره می‌گیرد.

شیوه به کارگیری مدل معادلات ساختاری

ایده اصلی در مدل معادلات ساختاری، تاثیر عمل جمع و ضرب روی اعداد است. همانطور که در مطلب مربوط به مباحث میانگین و واریانس خوانده‌اید، می‌دانیم که اگر همه مقدارها در یک عدد ثابت (مثل k) ضرب شوند، میانگین آن‌ها هم در همان مقدار ضرب خواهد شد. یعنی اگر داشته باشیم y=kx�=��، آنگاه خواهیم داشت ¯¯¯y=k¯¯¯x�¯=��¯. همچنین واریانس اعداد تبدیل یافته نیز در k2�2 ضرب خواهد شد یعنی می‌توان نوشت:

σ2y=k2σ2x��2=�2��2.

بر این اساس برای انحراف استاندارد داده‌های تبدیل شده هم رابطه زیر برقرار است:

sy=|k|sx��=|�|��

نکته‌ای که در اینجا به کار می‌آید، آن است که فرض کنید بین Y و X یک رابطه خطی به صورت Y=4X وجود دارد. در نتیجه واریانس Y باید ۱۶ برابر واریانس X باشد. با تصور معکوس این حالت می‌توان با مقایسه واریانس Yها با ۱۶ برابر واریانس Xها، آزمون مربوط مناسب بودن مدل Y=4X را با توجه به داده‌ها انجام داد.

این ایده را می‌توان برای چندین متغیر همبسته در گروهی از مدل‌های خطی به کار بست. هرچند در این حالت تعداد محاسبات و مدل‌های انتخابی زیاد هستند ولی اساس کار به همان شکل خواهد بود.

«بررسی وجود رابطه خطی بین متغیرها را می‌توان به بررسی واریانس و کووریانس آن‌ها تبدیل کرد.»

روش‌های آماری مختلفی برای بررسی چنین کاری وجود دارد که ساختار «ماتریس واریانس-کوواریانس» (Variance-Covariance Matrix) را تحلیل می‌کنند. به این ترتیب روش SEM طی مراحل زیر اجرا می‌شود:

1. متغیرهایی مرتبط و همبسته در مدل معرفی می‌شوند. این کار ممکن است بوسیله یک دیاگرام مسیر انجام شود.
2. براساس داده‌ها مشخص می‌شود که چه مقدار از رابطه بین متغیرها از طریق واریانس و کوواریانس متغیرها قابل تجزیه و تحلیل است.
3. به کمک آزمون فرض مشخص می‌شود که مدل انتخابی در بخش ۱ به چه میزان از لحاظ آماری بامعنا (Statistical Significant) است.
4. نتایج حاصل از آزمون فرض آماری و ضرایب یا پارامترهای مدل مشخص می‌شود.
5. براساس این اطلاعات، مشخص می‌شود که آیا داده‌ها توسط مدل قابل تفسیر هستند یا باید به معرفی مدل یا متغیرهای جدید دست زد.

هرچند محاسبات مربوط به روند SEM پیچیده و طولانی است ولی امروزه برنامه‌های زیادی به منظور انجام چنین محاسباتی موجود است. ولی آنچه حائز اهمیت محسوب می‌شود الگویی است که در انجام تحلیل SEM وجود دارد. برای راحتی کار مراحل بالا را در نمودار گردشی زیر می‌بینید.

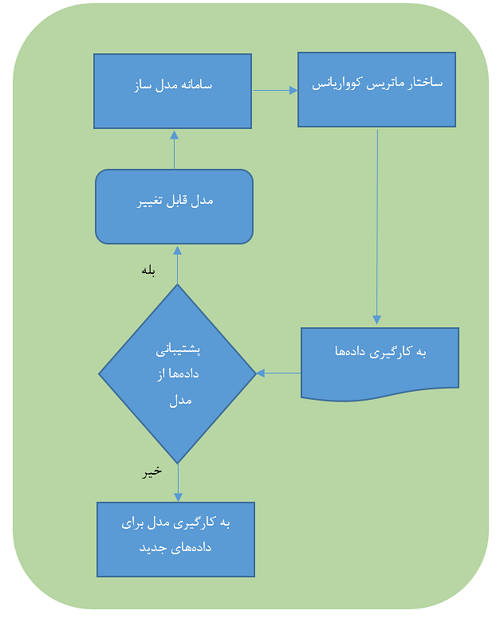
باید توجه داشت که هرگز بهترین مدل برای داده‌ها را نمی‌توان بوجود آورد. البته اگر برای داده‌های موجود بهترین مدل ساخته شود برای داده‌های جدید ممکن است مدل ایجاد شده مناسب نباشد. در این حالت مدل را «بیش‌برازش» (Overfitting) می‌نامند زیرا با در نظر گرفتن بیشترین تعداد متغیر در طراحی مدل، داده‌های موجود توسط مدل حفظ و رابطه‌شان به طور مصنوعی ایجاد شده است. همیشه رابطه‌های معرفی شده توسط مدل‌های آماری، تقریبی از مدل واقعی رابطه بین متغیرها هستند. زیرا براساس یک نمونه آماری از جامعه ساخته شده‌اند. بنابراین بهتر است به جای اصطلاح «بهترین برازش» (Best Fit) از «مناسب‌ترین برازش» (Good Fit) استفاده کنیم.https://beta.kaprila.com/a//templates_ver2/templates.php?ref=blog.faradars&id=string-1&t=string&w=760&h=140&background=fffff3&cid=2995531,2305,1012&wr=special,brother,brother&pid=54

نمودار مسیر و SEM

به منظور معرفی مدل در SEM از الگویی به نام «نمودار مسیر» (Path Diagram) استفاده می‌شود. این نمودار شبیه یک «نمودار گردش» (Flow Chart) است که در آن متغیرهای مرتبط بوسیله خطوطی در آن به یکدیگر متصل می‌شوند.

برای مثال فرض کنید که رابطه رگرسیونی خطی بین دو متغیر X و Y وجود دارد. یعنی داریم Y=aX+e که در آن a پارامتر مدل و e نیز خطای مدل محسوب می‌شوند. برای نمایش این رابطه در نمودار مسیر از شکل زیر استفاده می‌کنیم.

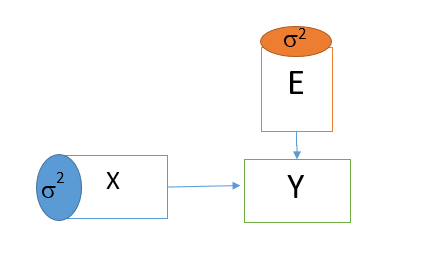
در این نمودار، همه متغیرهای مستقل در سمت چپ قرار دارند. متغیر مربوط به خطا نیز معرفی شده است. با توجه به میزان خطا در برآورد رابطه خطی بین دو متغیر X و Y متغیر دیگری که نقش مزاحم را دارد در مدل با E‌ دیده می‌شود. با مشخص شدن پارامترهای مدل برای هر متغیر مستقل، ضریب آن متغیر روی خط ارتباطی با متغیر وابسته دیده خواهد شد. این ضریب در صورتی که داده‌‌ها استاندارد شده باشند، می‌تواند به عنوان میزان اهمیت این متغیر در پیش‌بینی متغیر وابسته در نظر گرفته شود.

در هنگام معرفی مدل، ممکن است «متغیرهای پنهان» (Latent Variable) نیز در آن ایجاد شود. متغیر پنهان،‌ بدون آنکه در مرحله جمع‌آوری داده‌ها به عنوان یک متغیر تعریف شده باشد، به علت وجود رابطه بین متغیرهای مستقل ممکن است،‌ توسط روند SEM معرفی شود.

مثلا در بررسی قیمت خودرو با توجه به ویژگی‌هایی آن ممکن است حجم موتور، قدرت موتور و مصرف سوخت به عنوان متغیرهای مستقل اندازه‌گیری شده باشند ولی در واقعیت متوجه شویم که بین آن‌ها رابطه شدیدی وجود دارد و عملا به کارگیری آن‌ها در مدل رگرسیونی مناسب نیست. بنابراین ترکیبی خطی از آن‌ها را به عنوان متغیر پنهان که از ابتدا قابل اندازه‌گیری نبوده است در مدل اضافه می‌کنیم.

ویژگی موتوری=a × حجم موتور+b × قدرت موتور+c× مصرف سوخت

همچنین عامل دیگری به نام راحتی خودرو که به متغیرهای حجم اتاق و حجم صندوق عقب وابسته است، به عنوان یک متغیر پنهان دیگر در مدل حضور یابد.

راحتی خودرو=d × حجم اتاق+e × حجم صندوق عقب

این عوامل باعث می‌شوند که بین مولفه‌های جدید به عنوان متغیرهای پنهان کمترین وابستگی وجود داشته باشد و مدل حاصل از آن‌ها از اعتبار بیشتری برخوردار خواهد بود.

محاسبات مربوط به معادلات ساختاری در اغلب موارد در نرم‌افزارهای آماری AMOS یا نرم‌افزار لیزرل (LISREL) صورت می‌گیرد.

برگرفته از سایت فرادرس

• برای مشاهده لیست همه ی  پرسشنامه های استاندارد لطفا همین جا روی پرسشنامه استاندارد  کلیک فرمایید.
• تحلیل داده های آماری برای پایان نامه و مقاله نویسی ،تحلیل داده های آماری شما با نرم افزارهای کمی و کیفی ،مناسب ترین قیمت و کیفیت عالی انجام می گیرد.نرم افزار های کمی: SPSS- PLS – Amosنرم افزار کیفی: Maxqudaتعیین حجم نمونه با:Spss samplepower
• روش های تماس:Mobile :  09143444846  واتساپ – تلگرام کانال
• تلگرام سایت: برای عضویت در کانال تلگرام سایت اینجا کلیک کنید(البته قبلش فیلتر شکن روشن شود!!) مطالب جالب علمی و آموزشی در این کانال درج می گردد.