در بسیاری از تکنیک های آماری، نرمال بودن توزیع داده ها یک پیش فرض است.

وقتی که داده ها از توزیع نرمال پیروی نکنند، ممکن است استفاده از این روش های آماری، منجر به نتیجه گیری اشتباه گردد.

بنابراین آزمون نرمال بودن داده ها اهمیت می یابد.

برخی از تحلیل ها و روش های آماری که پیش شرط نرمال بودن توزیع داده ها و یا باقیمانده های مدل برای آن ها وجود دارد عبارتند از:

آزمون های تی استودنت (تک نمونه ای و دو نمونه ای زوجی و وابسته)
آنالیز واریانس (ANOVA)
آزمون های معناداری ضرایب در رگرسیون
آزمون فیشر برای همگنی واریانس جوامع
آزمون همبستگی پیرسون

توزیع نرمال، مهم ترین توزیع آماری است هم به جهت اینکه پیش فرض بسیاری از

روش های آماری است ( در عمل پدیده های مختلفی از قانون نرمال پیروی می کنند و این توزیع با توزیع های مختلفی ارتباط پیدا می کند)

و نیز به سبب قضیه مهم حد مرکزی.

در بسیاری از موارد در صورت وجود نمونه به اندازه کافی، جهت تخمین برخی از احتمالات،

می توان از این توزیع بهره برد (به این معنا نیست که نمونه های بزرگ از توزیع نرمال پیروی می کنند بلکه با افزایش

حجم نمونه، توزیع میانگین داده ها و یا برخی آماره های دیگر تحت شرایطی به نرمال گرایش دارد).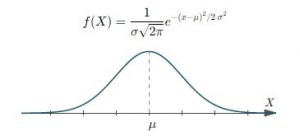

توزیع نرمال

برای بررسی نرمال بودن داده ها از دو روش کلی می توان بهره برد

روش توصیفی شامل نمودارها و بررسی شاخص های آماری
روش استنباطی شامل آزمون فرض ها

روش های توصیفی در بررسی نرمال بودن داده ها:

برای بررسی نرمال بودن توزیع داده ها،

ابتدا باید این نکته را توجه داشت که داده هایی که به دنبال بررسی توزیع احتمالی آن هستیم باید کمی و با مقیاس فاصله ای یا نسبی باشند (برای آشنایی با مقیاس های آماری اینجا کلیک کنید).

بنابراین داده هایی که غیر از این باشند،

مثلاً از نوع کیفی اسمی یا کیفی ترتیبی، مثل داده های جمع آوری شده از پرسشنامه با طیف لیکرت، به هیچ وجه نمی توانند از توزیع نرمال پیروی کنند،

حتی اگر برخی از روش ها مثل رسم هیستوگرام داده ها (رسم هیستوگرام برای این داده ها اشتباه است و باید از نمودار میله ای استفاده شود)، توزیع نرمال را تایید کند.

الف) رسم هیستوگرام داده ها و مقایسه آن با منحنی چگالی توزیع نرمال

رسم هیستوگرام داده ها به همراه منحنی توزیع نرمال کمک زیادی به تشخیص نرمال بودن توزیع داده ها می کند.

معمولاً با این روش می توان نرمال نبودن توزیع داده ها و دلایل آن را مشاهده کرد.

اگر هیستوگرام داده ها به توزیع نرمال نزدیک بود آنگاه می توان به سراغ آزمون فرض رفت.

در شکل زیر هیستوگرام یک سری داده استاندارد شده، به همراه منحنی نرمال استاندارد رسم شده است.

توزیع داده ها به توزیع نرمال بسیار نزدیک است (داده ها از توزیع نرمال شبیه سازی شده است).

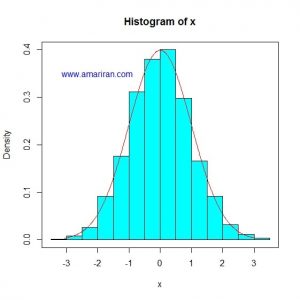
هیستوگرام داده ها و نمودار چگالی توزیع نرمال

نکته: برای رسم هیستوگرام داده ها، باید اول داده ها را استاندارد شده (منهای میانگین و تقسیم بر انحراف معیار)

و سپس با منحنی نرمال استاندارد مقایسه شود یا اینکه هیستوگرام داده های اصلی را با توزیع نرمال با میانگین و انحراف معیار داده ها مقایسه شود.

علاوه بر هیستوگرام، استفاده از نمودار جعبه ای نیز می تواند سودمند باشد.

ب) بررسی میزان کشیدگی و چولگی داده ها و مقایسه آن با مقدار این شاخص ها در توزیع نرمال

دو معیار کشیدگی و چولگی در داده ها در تشخیص نرمال بودن توزیع احتمالی داده ها، اهمیت زیادی دارد

و فلسفه برخی از آزمون ها نرمالیتی هم بررسی همین معیارهاست.

چولگی به میزان عدم تقارن منحنی فراوانی داده ها نسبت به منحنی فراوانی توزیع نرمال استاندارد گفته می شود. در داده های نرمال، منحنی فراوانی به شکل زنگوله مانند و متقارن است به نحوی که می توان شکل را از وسط به دو نیم تقسیم کرد. ولی اگر تمرکز داده ها در یک سمت منحنی نسبت به سمت دیگر بیشتر باشد، نمودار فراوانی داده ها چوله است. اگر تمرکز به سمت راست باشد، چوله به چپ و اگر به سمت چپ باشد، چوله به راست گویند.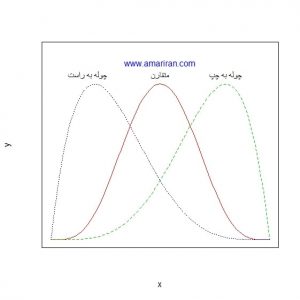

چولگی

برای محاسبه میزان چولگی سه ضریب چولگی معمولاً استفاده می شود،

ضریب چولگی اول پیرسون، ضریب چولگی دوم پیرسون و ضریب گشتاوری چولگی (آمار و احتمال مقدماتی بهبودیان).

همچنین کشیدگی به میزان برجستگی منحنی فراوانی داده ها نسبت به منحنی فراوانی توزیع نرمال استاندارد گفته می شود.

معمولاً در محاسبه میزان چولگی و کشیدگی یک نمونه از فرمول های زیر استفاده می شود:

$b= \frac{\mu_3}{s^3}=\frac{\frac{1}{n}\sum_{i=1}^n (x_i-\bar{x})^3} {\sqrt{\frac{1}{n-1}\sum_{i=1}^n (x_i-\bar{x})^2}^3}$

$\frac{.}{.}$

$k=\frac{\mu_4}{s^4}-3=\frac{\frac{1}{n}\sum_{i=1}^n (x_i-\bar{x})^4}{(\frac{1}{n-1}\sum_{i=1}^n (x_i-\bar{x})^2)^2}-3$

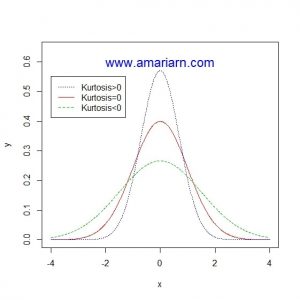
ج) رسم نمودار چندک – چندک و احتمال – احتمال

یکی دیگر از روش های بررسی نرمال بودن داده ها، نمودار چندک – چندک و احتمال – احتمال است.

ایده نمودار چندک – چندک مقایسه چندک های نمونه ای داده ها و چندک های توزیع موردنظر است. در اینجا با توزیع نرمال استاندارد مقایسه صورت می گیرد.

اگر داده ها از توزیع نرمال پیروی کنند، انتظار می رود که نمودار پراکنش چندک های نمونه ای داده ها در مقابل چندک های توزیع نرمال استاندارد در راستای یک خط راست قرار گیرند

(نیاز به استاندارد کردن داده ها نیست).

برای درک فلسفه ایده این روش فرض کنید $X_1, X_2, \dots , X_n$ یک نمونه تصادفی از توزیع نرمال

با میانگین $\mu$ و انحراف معیار $\sigma$ در این صورت:

$Z_i = (X_i-\mu) / \sigma , i=1, 2, \dots, n$

استاندارد شده داده ها و دارای توزیع نرمال استاندارد است.

اگر $Z_{(1)}, Z_{(2)}, \dots, Z_{(n)}$ مرتب شده ها باشند

به نحوی که $Z_{(1)} \leq Z_{(2)} \leq \dots \leq Z_{(n)}$ و $Z_{(i)}$ ها چندک ام نمونه هستند.

از طرفی تبدیل استاندارد ساز داده ها، نگاشتی صعودی است بدین معنی

که اگر آنگاه $(x-\mu)/ \sigma<(y-\mu)/ \sigma$ بنابراین می توان نوشت:

$Z_{(i)} = (X_{(i)}-\mu) / \sigma , i=1, 2, \dots, n$

زیرا:

$Z_{(1)} \leq Z_{(2)} \leq \dots \leq Z_{(n)} \Longleftrightarrow X_{(1)} \leq X_{(2)} \leq \dots \leq X_{(n)}$

به عبارت دیگر چون تبدیل استاندارد ساز یک تبدیل صعودی است،

چه اول داده ها را مرتب کرده و سپس تبدیل بزنیم و چه تبدیل زده

و سپس داده های حاصل را مرتب کنیم، در هر دو صورت نتیجه یکسان خواهد بود.

اگر داده ها از توزیع نرمال پیروی کنند، انتظار داریم که $Z_{(i)}$ با چندک ام توزیع نرمال استاندارد تقریباً برابر باشند.

یعنی $Z_{(i)} \simeq q_{i/n}$ . از طرفی به جای $q_{i/n}$ بهتر است از $q_{(i-0.5)/n}$ یا $q_{i/(n+1)}$ استفاده کرد.

بنابراین $X_{(i)} \simeq \sigma q_{(i-0.5)/n}+\mu$ . که معادله یک خط راست با عرض از مبدا $\mu$ و شیب $\sigma$ است.

پس اگر توزیع داده ها از توزیع نرمال پیروی کند انتظار می رود که نمودار پراکنش چندک های نمونه ای

و چندک های توزیع نرمال در راستای خطی راست باشد.

نکته: اگر نمودار چندک – چندک، نیمساز ربع اول دستگاه مختصات باشد، توزیع داده ها نرمال استاندارد است.

نکته: از این روش می توان در بررسی برازش توزیع های دیگر به داده ها نیز استفاده کرد.

کافیست به چندک های نمونه ای داده ها در مقابل چندک های توزیع موردنظر بررسی شود.

نکته: در نمودار چندک – چندک لزوماً نیاز به استاندارد سازی داده ها نیست،

طبق آنچه که گفته شد اگر چندک های نمونه ای در مقابل مقادیر مورد انتظارشان در توزیع نرمال استاندارد رسم شود،

انتظار می رود که یک خط راست تشکیل شود؛

حال اگر داده ها استاندارد شود، در صورت نرمال بودن داده ها خط مورد نظر نیمساز ربع اول است

ولی اگر استاندارد نشود، خطی با عرض از مبدأ برابر با میانگین داده ها و شیبی برابر با انحراف معیار داده ها تشکیل می شود.

در روش رسم نمودار احتمال – احتمال نیز مقادیر تابع توزیع تجربی داده ها در مقابل مقادیر مورد مورد انتظار تابع توزیع موردنظر (در اینجا توزیع نرمال) رسم می شود.

در صورتی که توزیع داده ها نرمال باشد، انتظار می رود که نمودار حاصل در امتداد یک خط راست (نیمساز ربع اول) باشد.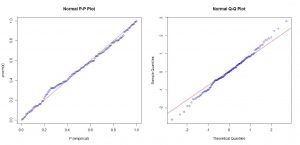

P-P plot & Q-Q plot

آزمون های آماری بررسی نرمال بودن توزیع داده ها

برای بررسی نرمال بودن توزیع داده ها، آزمون های زیادی پیشنهاد شده است از جمله:

اندرسون – دارلینگ، کلوموگروف – اسمیرنوف، شاپیرو – ویلک، جارکو – برا، لیلیفورس، نیکویی برازش کای دو، دی آگوستینو و… .

استفاده از آزمون های کلوموگروف – اسمیرنوف، شاپیرو – ویلک و اندرسون – دارلینگ عمومیت بیشتری دارد.

با افزایش حجم نمونه انتظار می رود که توان آزمون ها نیز بیشتر شود ولی از بین این آزمون ها، معمولاً شاپیرو – ویلک بیشترین توان و کلوموگروف – اسمیرنوف کمترین توان را دارد.

آزمون های نرمالیتی از لحاظ فلسفه آزمون به سه دسته کلی تقسیم بندی می شوند:

آزمون هایی که تابع توزیع تجربی داده ها با تابع توزیع نرمال مقایسه می کنند

(مثل کلوموگروف – اسمیرنوف)، آزمون هایی که براساس یک رابطه رگرسیونی و یا تحلیل همبستگی

بین آماره های ترتیبی و مقادیر مورد انتظارشان شکل گرفته اند (مثل شاپیرو – ویلک)

و آزمون هایی که براساس مقایسه شرایط عمومی داده ها با توزیع نرمال مثل چولگی و کشیدگی شکل گرفته اند (مثل دی آگوستینو).

نکته: آزمون هایی که در اکثر نرم افزارهای آماری تحت عنوان آزمون کلوکوگروف – اسمیرنوف

برای بررسی توزیع نرمال آمده است در واقع شکل اصلاح شده این آزمون برای بررسی نرمال بودن توزیع داده هاست

که در برخی منابع این نوع آزمون تحت عنوان آزمون لیلیفورس یاد می شود.

آزمون لیلیفورس در بررسی نرمالیتی نسبت به آزمون کلی کلوموگروف – اسمیرنوف توان بالایی دارد

که به همین خاطر در اکثر نرم افزارهای آماری در کنار آزمون شاپیرو – ویلک گنجانده شده است.

بیشترین توان های آزمون نرمالیتی در بین چهار آزمون متداول به ترتیب متعلق

به شاپیرو – ویلک، اندرسون – دارلینگ، لیلیفورس و کلوموگروف – اسمیرنوف است.

نکته: فلسفه آزمون شاپیرو – ویلک شبیه به فلسفه نمودار چندک – چندک است.

در این آزمون یک رابطه رگرسیونی بین آماره های ترتیبی داده ها و مقادیر مورد انتظار آماره های ترتیبی توزیع نرمال

در نظر گرفته می شود و آماره آزمون، چیزی شبیه به ضریب تعیین در رگرسیون است که هر چقدر بیشتر باشد نشان دهنده نزدیکی توزیع داده ها به توزیع نرمال است و مقادیر کوچک آماره آزمون باعث

رد فرض صفر (نرمال بودن توزیع داده ها) می شود.

نکته:برای اجرای آزمون شاپیرو – ویلک تعداد نمونه حداقل ۳ و حداکثر ۵۰۰۰ باید باشد

(نقاط بحرانی این آزمون تا حجم نمونه ۵۰۰۰ محاسبه شده است).

نکته: گاهی این مطلب به چشم می خورد که گفته می شود آزمون شاپیرو – ویلک برای

نمونه های کمتر از ۵۰ بسیار مناسب است. توان این آزمون با افزایش حجم نمونه افزایش می باید

و برعکس این مطلب، در تعداد نمونه کم، این آزمون توان قابل قبولی ندارد.

نقاط بحرانی این آزمون در ابتدا برای حجم نمونه تا ۵۰ (Shapiro and Wilk; 1965) و

در مقاله ای دیگر تا حجم نمونه ۵۰۰۰ محاسبه شده است. لذا در برخی از مقالات، توان این آزمون تا حجم نمونه ۵۰ مورد ارزیابی قرار گرفته و این گمان به وجود آمده که آزمون شاپیرو – ویلک برای نمونه کمتر از ۵۰ مناسب است.

نکته: مقایسه توان آزمون ها بستگی به شرایطی مثل چولگی و کشیدگی و حجم نمونه دارد

و در شرایط مختلف ممکن است کارایی آزمون ها با هم متفاوت باشد.

عموماً آزمون های نرمالیتی برای حجم نمونه بیشتر از ۲۰۰ توان معقولی دارند

به همین خاطر توصیه می شود اگر حجم نمونه کمتر از این مقدار باشد از روش های توصیفی استفاده شود.

نکته: آزمون کلوموگروف – اسمیرنوف به نقاط پرت حساسیت زیادی ندارد

ولی در مقابل آزمون شاپیرو – ویلک به داده های پرت حساس است.

نکته: در نرم افزار SPSS دو آزمون شاپیرو – ویلک و آزمون کلوموگروف – اسمیرنوف قابل انجام است

و در نرم افزار Minitab نیز علاوه بر این دو آزمون، امکان انجام آزمون اندرسون – دارلینگ وجود دارد.

در نرم افزار R نیز در بسته stats دو آزمون کلوموگروف – اسمیرنوف

و شاپیرو – ویلک قابل انجام است

و در بسته nortest آزمون های اندرسون – دارلینگ،

لیلیفورس (حالت اصلاح شده آزمون کلوموگروف برای آزمون نرمالیتی)،

کای دو پیرسون، شاپیرو – فرانسیا و آزمون کرامر – وان–میسز قابل انجام است.

در بسته fBasics نیز امکان انجام آزمون های جارکو – برا و دی آگوستینو وجود دارد.

برگرفته از آمار ایران

برای مشاهده لیست همه ی پرسشنامه های استاندارد لطفا همین جا روی پرسشنامه استاندارد کلیک فرمایید.

تحلیل داده های آماری برای پایان نامه و مقاله نویسی ،تحلیل داده های آماری شما با نرم افزارهای کمی و کیفی ،مناسب ترین قیمت و کیفیت عالی انجام می گیرد.

نرم افزار های کمی: SPSS- PLS – Amos

نرم افزار کیفی: Maxquda

تعیین حجم نمونه با:Spss samplepower

روش های تماس:

Mobile : 09143444846 واتساپ – تلگرام

Telegram: @abazizi

E-mail: abazizi1392@gmail.com

وبلاگ ما

برای تحلیل داده های آماری با کیفیت بالا و قیمت مناسب همین جا کلیک کن.

پژوهشگاه علمی (تحلیل آماری و پرسشنامه استاندارد )

بررسی توصیفی و استنباطی نرمال بودن داده های تحقیق؟ آیا استفاده از آزمون های آماری برای بررسی نرمالیتی هر نوع داده ای مناسب است؟