آموزش پیشرفته sPSS

انواع مدل هاي معادلات ساختاري و کاربرد آن ها

پاسخ دهید

انواع مدل هاي معادلات ساختاري و کاربرد آن ها

در این مقاله به تشریح انواع مدل های معادله ساختاری و کاربرد آنها می پردازیم.

تحلیل آماری

1- مدل های با معرف های چندگانه و علل چندگانه

معرف های چندگانه و علل چندگانه نوع خاصی از مدل های معادله ساختاری را معرفی می کند و به طور مخفف با

MIMIC (Multiple Indicator and Multiple Causes)

نشان داده می شود. مدل های MIMIC شامل کاربرد متغیرهای پنهانی است که بوسیله متغیرهای مشاهده شده پیش بینی می شوند. این موضوع را با مثالی از یورسکوگ و سوربوم (1996) بیان می کنیم که در آن یک متغیر پنهان (مشارکت اجتماعی) بوسیله رفتن به کلیسا، عضویت های گروهی و دیدار دوستان تعریف شده است. همچنین این متغیر بوسیله متغیرهای مشاهده شده درآمد، اشتغال و تحصیلات پیش بینی می شود.

متغیر پنهان مشارکت اجتماعی با پیکان هایی به سه معرف متصل شده است که هرکدام دارای مقداری خطای اندازه گیری هستند. همچنین سه پیکان از متغیرهای مشاده شده به سمت متغیر مشارکت اجتماعی نشانه رفته است. این متغیرهای مشاهده شده با یکدیگر همبستگی دارند. پس از بررسی معناداری متغیرها در صورت لزوم متغیرهای غیرضروری از مدل حذف می شوند.

2- مدل های گروه های چندگانه

تحلیل مدل های گروه های چندگانه با بررسی مدل های اندازه گیری و یکسانی اندازه گیری بین گروه ها آغاز می شود . چنین تحلیلی قبل از بررسی فرضیه های وجود تفاوت معنادار در ضرایب ساختاری بین گروه ها ضروری است. کاربرد این مدل شامل آزمون تفاوت بین برآورد پارامترها برای گروه های چندگانه می باشد.

به عنوان نمونه می توانیم به مثال ارائه شده توسط آربوکل و تکه (1999) اشاره کنیم. در این تحقیق تفاوت های ارزیابی از جذابیت و ارزیابی از توان آکادمیک بین دو گروه دختران و پسران مورد بررسی قرار گرفته است.

3-  مدل های چند سطحی

مدل های چندسطحی در مدل سازی معادله ساختاری به علت ماهیت سلسله مراتبی داده ها در یک طرح تحقیقی آشیانه ای به این نام خوانده می شوند. به عنوان مثال پیشرفت تحصیلی یک دانشجو در کلاس ها پایه ریزی شده است، بنابراین دانشجویان در کلاس ها آشیان شده، معلمان درمدارس آشیان شده هستند و مدارس در مناطق آشیان شده اند. طرح پژوهشی آشیانه ای با یک طرح پژوهشی متقاطع متفاوت است.

علاقه ما در این نوع از طرح ها، با ملاحظه ماهیت خوشه ای شده داده ها، به اثرات در سطوح متفاوت است. EQS دارای سه روش اجرای مدل چند سطحی بر اساس یک متغیر خوشه ای است که عبارتند از :

  • الف) حداکثر درستنمایی با استفاده از الگوریتم انتظار/ ماکزیمم کردن.
  • ب) برآورد موتن مبتنی بر حداکثر درستنمایی
  • ج) مدل خطی سلسله مراتبی.

روش چندسطحی ML با استفاده از برآورد حداکثر درستنمایی، الگوریتم EM را در دو گام به منظور برآورد پارامترها و خطاهای معیار به کار می برد. الگوریتم اول گام انتظار است(E) که در آن ماتریس های کواریانس درون و بین سطحی با استفاده از تکرار برآورد می شوند. گام دوم به حداکثر رسانی (ماکزیمم سازی) است که در آن اگر معیار همگرایی برقرار باشد، برآوردهای حداکثر درستنمایی و خطاهای معیار تولید می شوند.

تحلیل چندسطحی با ML تنها برای مدل های دوسطحی طراحی شده است. تفسیر مدل های چندسطحی که بیشتر از دو سطح آشیان شده دارند مشکل است. اما با این حال مدل های خطی سلسله مراتبی در رگرسیون با سه سطح از متغیر مشاهده شده تحلیل شده اند.

مدل های خطی سلسله مراتبی در EQS برای تحلیل تا 5 سطح با استفاده از متغیرهای پنهان طراحی شده اند. در مدل های خطی سلسله مراتبی ابتدا معادله سطح اول معادله سطح اول برای هر خوشه اجرا شده و پارامترهای برآورد شده ذخیره می شوند و سپس برای استفاده در معادله سطح دو مورد استفاده قرار می گیرند. بنابراین معادله سطح دوم داده های خود و همچنین پارامترهای برآورد شده از سطح اول را مورد استفاده قرار می دهد.

مدل چند سطحی خطی سلسله مراتبی در EQS مشابه برنامه های چند سطحی حداکثر درستنمایی و برآورد موتن بر مبنای حداکثر درستنمایی است به جز اینکه مجموعه دومی از داده ها نیز در آن تعریف می شوند.

4- مدل های ترکیبی

مدل های ترکیبی در مدل سازی معادلات ساختاری شامل تحلیل متغیرهای مشاهده شده ای است که از دو نوع مقوله ای و پیوسته هستند. EQS امکانی را فراهم می آورد که دو نوع متغیرهای مقوله ای و پیوسته در مدل حضور داشته باشند.

5- مدل میانگین های ساختمند

کاربرد مهم دیگر مدل سازی معادله ساختاری، آزمون تفاوت میانگین های گروهی برای متغیرهای مشاهده شده یا پنهان است. این کاربرد در واقع حالت توسعه یافته تحلیل پایه رویکرد واریانس است جایی که تفاوت میانگین ها برای متغیرهای مشاهده شده آزمون می شوند. آزمون تفاوت میانگین ها بین متغیرهای مشاهده شده در مدل سازی معادله ساختاری مشابه با تحلیل واریانس و کواریانس است.

در مورد آزمون مربوط به متغیرهای پنهان به عنوان مثال آزمون تفاوت میانگین متغیر پنهان توان شفاهی بین پسران دانشگاهی و غیر دانشگاهی در پایه های پنجم و هفتم را می توان در نظر گرفت. در این مثال نمرات افراد در خواندن و نوشتن، متغیر پنهان را در پایه های پنجم و هفتم می سازد.

6- مدل های چند خصیصه ای-چند روشی

این مدل ها با هدف نشان دادن خصایص چندگانه ارزیابی شده به وسیله سنجه های چندگانه مورد استفاده قرار می گیرند. به عنوان مثال می توان از پیشرفت و انگیزه دانش آموزان (خصیصه ها) نام برد که به وسیله نمره دهی معلمان و نمره دهی خود دانش آموزان (روش ها) ارزشیابی شده اند. این مدل ها اطلاعاتی را برای تعیین اعتبار سازه تدارک می بینند.

ماتریس چندخصیصه ای-چند روشی ضرایب اعتبار همگرا، ضرایب اعتبار ممیز و ضرایب قابلیت اعتماد را در طول قطر منعکس می کند. ضرایب قابلیت اعتماد نشان دهنده سازگاری درونی نمرات بر روی ابزار است و بنابراین باید حدودا بین 0.85 تا 0.95 یا بالاتر قرار گیرد. ضرایب اعتبار ممیز، همبستگی های بین سنجه های خصایص مختلف (سازه ها) با استفاده از روش یکسان (ابزار) است و بنابراین انتظار می رود بسیار پایین تر از ضرایب اعتبار همگرا و یا ضرایب قابلیت اعتماد ابزار باشد.

7- مدل یگانگی همبسته

این مدل ها توسط مارش و گریسون (1995) و وتکه (1996) به عنوان جایگزینی برای مدل های سنتی چندخصیصه ای-چند روشی طرح شده اند. در مدل های یگانگی همبسته هر متغیر به عنوان یک عامل خصیصه و یک جمله خطا، اثر پذیرفته و عامل های روشی نیز وجود ندارند. اثرات روش به وسیله جملات خطای همبسته هر متغیر به حساب می آیند.جملات خطای همبسته تنها بین متغیرهای سنجش شده به وسیله روش مشابه وجود دارند.

انواع متفاوتی از مدل های یگانگی همبسته می توانند تحلیل شوند. به عنوان مثال می توان به از یک عامل عام با یگانگی همبسته، دو عامل همبسته با یگانگی غیرهمبسته و دو عامل غیرهمبسته با یگانگی همبسته نام برد.  مارش و گریسون نشان می دهند که وجود کاهش معنادار در برازش بین یک مدل با خصایص همبسته اما جملات غیر همبسته و یک مدل با خصایص همبسته همراه با جملات خطای همبسته، نشانه وجود اثرات روشی است.

8- مدل های عاملی مرتبه دوم

این مدل ها هنگامی طرح می شوند که مدل های مرتبه اول به وسیله ساختار عاملی مرتبه بالاتر تبیین شوند. به عنوان مثال براساس داده های هولتزینگر و اسواینفورد نه متغیر روانشناختی، تعریف کننده سه عامل مشترک (بصری، شفاهی و سرعت) هستند. این سه عامل به نوبه خود عانل یگری به نام توان را تعریف می کنند. در برنامه Lisrel متغیر توان به عنوان یک متغیر پنهان معرفی می شود.

9- مدل های تعاملی

در مثال های قبلی فرض بر این بود که روابط موجود در مدل ها خطی هستند، به این معنا که همه روابط بین متغیرهای مشاهده شده و پنهان می توانند به وسیله معادلات خطی نشان داده شوند. هرچند که کاربرد اثرات تعاملی و غیرخطی در مدل های رگرسیونی عمومیت دارد، ارائه فرضیه های تعاملی در مدل های مسیر در حداقل است و مثال های بسیار کمی از مدل های عاملی غیرخطی تدارک دیده شده است. در واقع برای چندین دهه مدل سازی معادلات ساختاری برمبنای روابط ساختاری خطی قرار داشته است. اکنون مدل های معادله ساختاری با اثرات تعاملی امکان پذیر است.

در مدل سازی معادلات ساختاری اکنون می توانیم اثرات اصلی و اثرات تعاملی متغیرهای پنهان را آزمون کنیم. در هر حال چندین نوع از اثرات تعاملی وجود دارد. اثرات حاصلضرب متغیرهای مشاهده شده، غیرخطی، مقوله ای و حداقل مربعات دو مرحله ای.

رویکردهای متفاوتی را می توان برای بررسی اثرات تعاملی به کار برد، در ادامه این روش ها معرفی می شوند:

1-9- رویکرد متغیر پیوسته

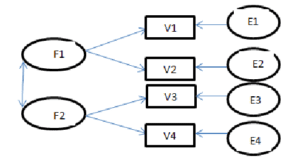
کنی و جود (1984) روشی را برای آزمون تعامل میان متغیرهای پنهان براساس حاصلضرب های متغیرهای مشاهده شده طرح کرده اند. روش آن ها این امکان را فراهم می آورد که پژوهشگر هر دو نوع جملات درجه دوم و تعاملی را در میان متغیرهای پنهان وارد کند. به عنوان مثال اگر F1 بوسیله متغیرهای مشاهده شده X1 و X2 و F2 بوسیله متغیرهای مشاهده شده X3 و X4 تعریف شده اند، آنگاه تعامل متغیرهای پنهان به عنوان F3 می تواند بوسیله حاصلضرب های متغیرهای مشاهده شده مربوطه تعیین شود؛ یعنی X1X3 ، X1X4 ، X2X3 ، X2X4 . در این رویکرد متغیر پنهان تعاملی F3 می تواند در کنار متغیرهای پنهان اصلی F1 و F2 در معادله ساختاری وارد شود.

2-9- رویکرد متغیر مقوله ای

در این رویکرد نمونه های متفاوتی برحسب سطوح متفاوت متغیرهای تعاملی تعریف شده اند. منطق زیربنایی چنین است که چنانچه اثرات تعاملی وجود داشته باشند، هم اثرات اصلی و هم اثرات تعاملی می توانند با استفاده از نمونه ای متفاوت، به منظور آزمون تفاوت بین مقادیر عرض از مبدأ و ضریب زاویه تدوین شوند. دستیابی به چنین مدلی به وسیله اجرای دو مدل متفاوت امکان پذیر است. مدل اثرات اصلی برای تفاوت های گروهی در حالی که ضریب زاویه را ثابت نگه می داریم و مدل اثرات تعاملی برای تفاوت های گروهی در حالیکه مقادیر عرض از مبدأ و ضریب زاویه برآورد می شوند.

3-9- رویکرد حداقل مربعات دو مرحله ای

بولن (1996و1995) نشان داد که مدل های معادیه ساختاری غیرخطی می توانند به وسیله متغیرهای ابزاری در حداقل مربعات دو مرحله ای برآورد شوند. این روش از دو مرحله تشکیل شده است. در مرحله اول هریک از متغیرهای کمی برونزا در مدل رگرسیون می شوند و مقدار پیش بینی شده از این رگرسیون حاصل می شود.

در مرحله دوم رگرسیون هدف به طور معمول تخمین زده می شود و هر یک از متغیرهای برونزا با مقدار پیش بینی شده از مرحله اول جایگزین می شود. برآوردهای حداقل مربعات دو مرحله ای و خطاهای معیار آن ها بدون تکرار حاصل می شوند و بنابراین اطلاعاتی را بدست می دهد برای پاسخ به این سؤال که آیا مدل تدوین شده قابل دفاع هست یا خیر؟

4-9-  مدل های انحنایی رشد پنهان

تحلیل واریانس سنجه های تکرار شده به طور گسترده ای با استفاده از متغیرهای مشاهده شده برای آزمون آماری تغییرات در طول زمان مورد استفاده قرار گرفته اند. مدل سازی معادله ساختاری تحلیل داده های طولی را توسعه داده تا رشد متغیر پنهان را در طول زمان در برگیرد، در حالیکه هم تغییرات منفرد و هم تغییرات طولی را با استفاده از ضریب زاویه و مقادیر عرض از مبدأ به مدل درمی آورد. تحلیل انحنایی رشد پنهان به لحاظ مفهومی مشتمل بر دو تحلیل متفاوت است.

تحلیل اولیه سنجه های تکرار شده در طول زمان، که به طور خطی یا غیرخطی به شکل فرضیه درآمده است.

تحلیل دوم شامل استفاده از پارامترهای منفرد(مقادیر ضریب زاویه و عرض از مبدأ) برای تعیین تفاوت رشد از یک خط مبنا است. مدل انحنایی رشد پنهان تفاوت ها را در طول زمان منعکس کرده و میانگین ها (عرض از مبدأ) و نرخ تغییرات(ضریب زاویه) را در دو سطح فردی و گروهی به حساب می آورد.

در هر حال این رویکرد نیازمند نمونه های بزرگ، داده های دارای توزیع نرمال چندمتغیره، فواصل زمانی مساوی برای همه آزمودنی ها و تغییراتی می باشد که در نتیجه یک پیوستار زمانی رخ می دهند.

5-9- مدل های عاملی پویا

نوعی از کاربردهای مدل سازی معادله ساختاری که شامل متغیرهای پنهان ثابت و غیرثابت در طول زمان، با خطای اندازه گیری تأخیری (همبسته) است به نام تحلیل عاملی پویا خوانده می شود. ویژگی این کاربرد از مدل سازی معادله ساختاری این است که ابزارهای اندازه گیری مشابهی برای آزمودنی های یکسانی در دو یا تعداد بیشتری از موقعیت های زمانی اجرا شده اند.

هدف این تحلیل ارزیابی تغییر در متغیر پنهان بین دو موقعیت مرتب شده، در ارتباط با برخی وقایع یا آزمایش ها است. هنگامی که ابزار اندازه گیری مشابهی در دو یا چند موقعیت زمانی به کار می روند، تمایلی برای وجود خطای اندازه گیری همبسته وجود دارد (خودهمبستگی) 

برگرفته از سایت اطمینان شرق

دیدگاهتان را بنویسید

نشانی ایمیل شما منتشر نخواهد شد. بخش‌های موردنیاز علامت‌گذاری شده‌اند *